3. El origen del ataque a Enigma. El BS4

Este artículo trata la importancia de la desencriptación de los Códigos Enigma y Lorenz alemanes por parte de los aliados gracias al trabajo analítico de multitud de matemáticos, cuyo resultado fue vital para la derrota de los nazis en la 2ª Guerra Mundial, acortando ésta al menos en dos años.

BS4: era la sección alemana del Biuro Szyfrów cuyo jefe era el mayor Maksymilian Ciężki.

 

Oficiales alemanes con un transceptor de radio y una máquina Enigma cifrando mensajes

 

Índice:

• 3.1. 1ª Etapa. De Poznań a Varsovia
• 3.2. 2ª Etapa. La aparición de Asché
• 3.3. El Método de las Permutaciones. Fundamentación Teórica
• Teoría de Permutaciones
• Teoría de Permutaciones (cont.)
• 3.4. 3ª Etapa. La amenaza de la invasión y la búsqueda de aliados
• 3.5 Reunión del bosque de Pyry
• El Ciclómetro
• Véase también

 

3.1. 1ª Etapa. De Poznań a Varsovia

Tras la 1ª Guerra Mundial, los aliados se encargaron de vigilar las comunicaciones germanas. Sin embargo a partir de 1926, comenzaron a interceptar mensajes cifrados mediante un nuevo método que desconocían hasta el momento. En medio de este desconcierto se encontraba el recientemente formado estado soberano de Polonia, el cual tenía al este a la Unión Soviética, un estado hambriento por expansionar su doctrina comunista fuera de sus fronteras, y al oeste Alemania, un estado que ansiaba recuperar los territorios cedidos a Polonia tras la guerra. En este clima de desconfianza, los polacos crearon su Oficina de Cifrado, el Biuro Szyfrów, a mediados de 1931, surgido de la unión de la Oficina de Radio-Inteligencia (Referat Radiowywiadu) y la Oficina Criptográfica Polaca (Referat Szyfrów Wlasnych), e integrada en la 2ª Sección del ejército polaco, siendo su máximo responsable el teniente coronel Gwido Langer (1894-1948), y el mayor Maksymilian Ciężki (1894-1948) el jefe de la sección encargada de desencriptar los mensajes cifrados alemanes. Ciężki conocía la Enigma comercial, sin embargo, no tenía acceso a la Enigma militar, claramente distinta debido a los cambios introducidos en ella, por lo que al desconocer su cableado interno, fue incapaz de iniciar un ataque efectivo a su cifrado.

En enero de 1929, el director de la Universidad de Poznań (actualmente Universidad Adam Mickiewicz) Zdzislaw Krygowski preparó una lista de 20 estudiantes de matemáticas de últimos cursos que recibieron un llamamiento del ejército para participar en un curso de criptología. Bajo el juramento por parte de estos alumnos de mantener toda la operación en secreto, el curso se impartiría durante dos noches a la semana en dicha Universidad por el ya nombrado mayor Maksymilian Ciężki, Antoni Palluth (1900-1944), un ingeniero empleado civil del Biuro Szyfrów, y el mayor Franciszek Pokorny, por entonces jefe del mismo, emparentado con el famoso criptólogo del ejército austríaco durante la 1ª Guerra Mundial, el capitán Herman Pokorny. El curso tenía como principal propósito servir de apoyo al Servicio de Inteligencia Polaco de Radio con el fin de descifrar los mensajes alemanes interceptados. La razón de la elección de la Universidad de Poznań fue fundamentalmente debido a que la región de Pomerania, situada al oeste de Polonia, formó parte de la Prusia oriental, desde 1793 hasta 1918, por lo que sus habitantes hablaban perfectamente el alemán, de hecho a finales del siglo XIX, la escuela era obligatoriamente impartida en lengua germana. La otra razón de esta elección fue que, aunque no era demasiado conocido, la universidad contaba con un Instituto de Matemáticas.

Figura14. Universidad de Poznań (1929)

Tras varias semanas, los estudiantes que asistieron a dicho curso fueron puestos a prueba para descifrar varios mensajes alemanes reales anteriores al uso de la Enigma que ya habían sido descifrados previamente. Con el fin de acotar su vocabulario se les daba una idea sobre el tema que trataba cada mensaje. Tras un par de horas, algunos estudiantes entre los que se encontraban Marian Rejewski (1905-1980), Jerzy Różycki (1909-1942) y Henryk Zygalski (1908- 1978), fueron capaces de descifrar los mensajes. A medida que el curso avanzaba, estos mensajes se fueron complicando paulatinamente, de modo que muchos estudiantes fueron abandonando el curso bien porque preferían dedicarse enteramente a sus estudios, o bien porque consideraban que no tenían suficientes habilidades para la criptología. Únicamente los tres estudiantes antes nombrados fueron capaces de compaginar sus estudios con el curso. Uno de los exámenes a los que fueron sometidos era una comunicación militar alemana entonces actual cifrada mediante el código denominado “Cifrado de Doble Transposición”. Los tres estudiantes, cada uno de manera independiente, fueron capaces de romper dicho código, poniendo de manifiesto que estaban dotados de ciertas habilidades criptológicas. Muy a su pesar, Rejewski tuvo que abandonar el curso antes de su finalización, puesto que recibió una beca para estudiar en la Universidad de Gotinga, sueño de cualquier estudiante de matemáticas, puesto que allí habían impartido clases eminencias como Gauss, Riemann, Dirichlet, Poincaré o Hilbert entre otros.

 

En el verano de 1930, Rejewski regresó a Poznań. Al finalizar el curso, los mejores estudiantes del mismo fueron invitados para colaborar con el Biuro Szyfrów cuyas oficinas estaban en los sótanos de la comandancia militar polaca equipadas con todo lo necesario para descifrar los mensajes alemanes. De forma general se permitía a los estudiantes compaginar sus tareas criptológicas con sus estudios, de manera que su trabajo en el Biuro Szyfrów se distribuía generalmente en doce horas semanales en el turno que ellos prefirieran, ya fuera diurno o incluso nocturno. La “cámara oscura” (como llamaban los estudiantes a los oficinas del Biuro) estaba en el puesto de la comandancia militar, tan sólo a unos pasos del Instituto de Matemáticas para que los estudiantes no tuvieran que perder demasiado tiempo en el trayecto y aprovechar así sus tiempos muertos. Rejewski comenzó a trabajar allí en el otoño de 1930.

Se formó de este modo un grupo de trabajo de jóvenes matemáticos, cuya principal tarea consistía en el descifrado de todo tipo de códigos alemanes. Los estudiantes recibían constantemente información de varias estaciones de radio dedicadas a interceptar mensajes cifrados de los alemanes quienes regularmente cambiaban sus claves, y rápidamente aprendieron incluso a aprovechar los errores cometidos por los operadores alemanes, como por ejemplo el hecho de que necesitaran mensajes de al menos 50 caracteres de longitud. Los estudiantes descubrieron que los alemanes caracterizaban estos mensajes más cortos con la letra “X” y a continuación codificaban el mismo. Sin embargo, a pesar de sus más que notables habilidades criptológicas, aparecieron unos cifrados que no podían romper independientemente de las técnicas utilizadas. El uso de la Enigma se había instaurado de forma total en el ejército alemán y era el momento de “profesionalizar” las tareas criptológicas de los estudiantes polacos. En el verano de 1932, el puesto de Poznań fue cerrado y Rejewski primero, y Różycki y Zygalski un poco después, comenzaron a trabajar como empleados del Biuro Szyfrów en Varsovia. Nacía así el BS4 y comenzaba la guerra contra Enigma.

 

3.2. 2ª Etapa. La aparición de Asché

Figura 15. Miembros del BS4

El trabajo del BS4 se basó fundamentalmente en el estudio de la repetición de patrones. El patrón más obvio de la encriptación de la Enigma era la clave de mensaje, que se codificada dos veces al principio de cada mensaje. Los alemanes habían exigido dicha repetición para prevenir posibles errores causados por las intermitencias de radio o fallos del operador, sin embargo no previeron que esto pondría en peligro la seguridad de la máquina. A pesar de que los polacos del BS4 realizarían un gran avance en el descubrimiento del funcionamiento de la Enigma mediante el análisis de los patrones de repetición, consiguiendo identificar que las cadenas de caracteres cifrados tenían una relación dependiente exclusivamente de la posición de los rotores de la máquina, al principio su principal limitación era su desconocimiento sobre la distribución del cableado interior de la máquina, ya que no contaban con ninguna máquina física del ejército alemán. Este hecho añadido a que los alemanes modificaban el cableado interior de las máquinas que adquirían con el fin de evitar posibles espionajes que comprometieran la integridad de sus comunicaciones, impidieron en primera instancia que los polacos del BS4, del que formaba parte el joven Rejewski entre otros, fueran capaces de descifrar los mensajes interceptados.

Existe un punto de vista erróneo que se repite sistemáticamente en multitud de publicaciones, y que no es otro que considerar que la ruptura del código de Enigma se produjo de una manera puntual, cosa que no fue así puesto que los polacos llevaron a cabo pequeños logros que se tradujeron finalmente en comprender el funcionamiento de la Enigma y consecuentemente establecer una estrategia eficaz para desentrañar el código de encriptación que la máquina escondía. El primer intento de búsqueda de la desencriptación del código Enigma llevaría en torno a cuatro meses, proceso que debía considerar dos cuestiones bien diferenciadas:

1. Por un lado la reconstrucción teórica de la Enigma militar. Los criptólogos polacos descubrirían primero la función del reflector (Umkehrwalze), tras lo cual reconstruyeron poco a poco todas conexiones existentes en la máquina, cuyos principales componentes eran el sistema de rotores (Chiffrierwalzen) que giraban sobre un eje común, y el panel de conexiones o clavijero. Esto supuso que los polacos fueran capaces de construir unas réplicas de la Enigma que hacían posible la lectura de los mensajes cifrados alemanes una vez se encontraran las claves de configuración de los rotores.
2. Por otro lado estaba el proceso de elaboración de los métodos para la reconstrucción de las claves de la Enigma basándose únicamente en los mensajes interceptados por las estaciones polacas de radiomonitoreo.

Es en este momento en el que hace su aparición la figura de Hans Thilo Schmidt, un corrupto y resentido funcionario de la Chiffrierstelle en Berlín, la oficina responsable de administrar las comunicaciones cifradas de Alemania. Schmidt, que sirvió en la 1ª Guerra Mundial y fue expulsado del ejército después de los recortes producidos en el mismo tras la firma del armisticio en Versalles, había entrado en la oficina de cifras a través de la intervención de su hermano Rudolf, un reputado oficial alemán con una trayectoria en ascenso al que parece ser que se le atribuye la idea de sugerir al alto mando del ejército alemán que se considerara la Enigma con el objetivo de salvaguardar la seguridad de las comunicaciones. Schmidt tenía fama de mujeriego y parece que le gustaba vivir por encima de las posibilidades que un puesto como el suyo le podía proporcionar. Fue entonces cuando a través de la embajada de Francia en Berlín, accedió a intercambiar información valiosa sobre el funcionamiento de Enigma a cambio de cuantiosas prebendas. Así fue como el servicio secreto francés, a través de la intermediación del entonces capitán Gustave Bertrand (1896-1976) y el agente secreto cuyo pseudónimo era Rex, obtuvo copia de varios documentos sobre el funcionamiento de la Enigma de manos de Schmidt el 8 de noviembre de 1931 en el Grand Hotel de Verviers, Bélgica.

 

Hans Thilo Schmidt

Se establecieron varias reuniones entre septiembre y octubre de 1932, en las que Schmidt, cuyo nombre en clave era Asché (pronunciación francesa de H), proporcionó los libros de códigos con todas las claves del día completas para 38 meses firmados por el teniente coronel Erich Fellgiebel (más tarde nombrado general y jefe de la sección de comunicaciones de la Wehrmacht), así como fotos de la máquina, aunque en ningún caso ninguna documentación sobre el cableado interno de los rotores. Sin embargo, muy a su pesar, los criptoanalistas franceses fueron incapaces de sacar partido a dicha información. Por ello, en virtud del tratado de colaboración que franceses y polacos habían firmado tras la 1ª Guerra Mundial, y dado que el Biuro Szyfrów estaba muy interesado en todos los asuntos relacionados con la Enigma, la inteligencia francesa decidió compartir esta información con sus homónimos polacos, lo que significó un punto de inflexión en el ataque al código de Enigma. Schmidt trabajó en la Chiffrierstelle hasta 1938. El 23 de marzo de 1943 sería arrestado y supuestamente reconoció su espionaje en julio de ese año. Finalmente se suicidaría el 19 de septiembre de 1943. 

 

El jefe del Biuro Szyfrów, Gwido Langer, tomó una desconcertante pero astuta decisión. No entregó en primera instancia los libros de claves a Rejewski hasta finales de 1932, consciente de que éstas no estarían disponibles en tiempos de guerra. De este modo obligó al propio Rejewski a entrenar sus capacidades criptoanalíticas en tiempo de paz en previsión del inminente conflicto bélico que inevitablemente estaba a punto de estallar. En este punto, Rejewski y sus colegas no tuvieron más remedio que agudizar su ingenio para buscar una manera de romper el código de la Enigma. Rejewski que contaba con alguna Enigma comercial buscó refugio en las matemáticas puras y abstractas, en particular en el estudio de las permutaciones dentro de la rama denominada como teoría de grupos. Uno de los pilares fundamentales para el análisis criptológico en general son el estudio de las repeticiones, en el caso de Enigma, Rejewski comenzó por estudiar los únicos patrones de repetición que conocía, la clave de los mensajes que se repetía al inicio de cada uno de ellos.

 

3.3. El Método de las Permutaciones. Fundamentación Teórica

A pesar de que la tesis de Marian Rejewski titulada Teoría de funciones periódicas dobles de segunda y tercera especie y sus aplicaciones, estaba más cerca del análisis que del álgebra, estaba muy familiarizado con la teoría de grupos, y conocía bastante bien las permutaciones. Desde un punto de vista formal, una permutación puede considerarse como una reordenación de elementos. Por ejemplo cuando ordenamos las lista de nuestros alumnos por orden alfabético de sus apellidos, o cuando barajamos un mazo de cartas, estamos realizando un cambio del orden de estos conjuntos que puede ser representado mediante una permutación.
Imaginemos por un instante que tenemos un conjunto de seis elementos: “a”, “b”, “c”, “d”, “e”, y “f” (Con la intención de seguir un esquema de exposición formal, notaremos en mayúsculas a las permutaciones y en minúsculas las letras del alfabeto).

Una permutación podría ser la siguiente:

• “a” se convierte en “c”, (“a” → “c”)
• “b” se convierte en “a”, (“b” → “a”)
• “c” se convierte en “b”, (“c” → “b”)
• “d” se convierte en “f”, (“d” → “f”)
• “e” se convierte en “d”, (“e” → “d”)
• “f” se convierte en “e”, (“f” → “e”)

De esta manera, la permutación que denominaremos P, transforma el conjunto ordenado (abcdef) en el conjunto ordenado (cabfde). Una manera de indicar la permutación es haciendo cadenas cíclicas, esto es, por un lado
“a” → “c”, “c” → “b”, “b” → “a”, y por otro
“d” → “f”,
“f” → “e”, “e” → “d”, de forma que tenemos dos ciclos cerrados de tres elementos cada uno de ellos. Podremos por lo tanto expresar la permutación P como:

P = (acb)(dfe)

 

Rejewski supo vislumbrar la conexión entre la matemática abstracta y teórica con el mecanismo de funcionamiento de la máquina Enigma a través de las permutaciones, esperando que la teoría de grupos fuera capaz de extraer alguna propiedad sencillamente asociable a la configuración de los rotores, reduciendo en gran medida el enorme número de posibilidades combinatorias de rotores, reflector y clavijero.

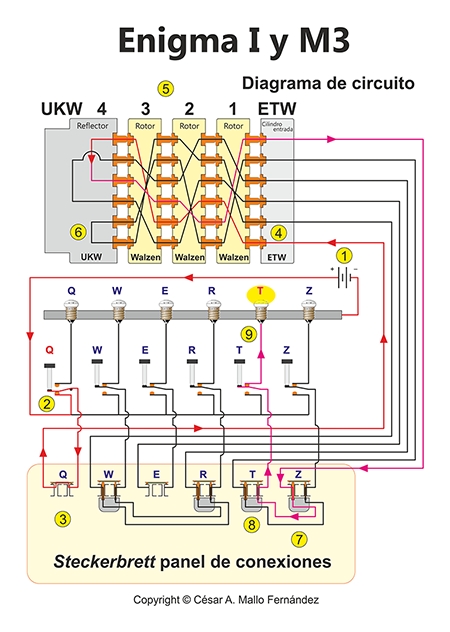
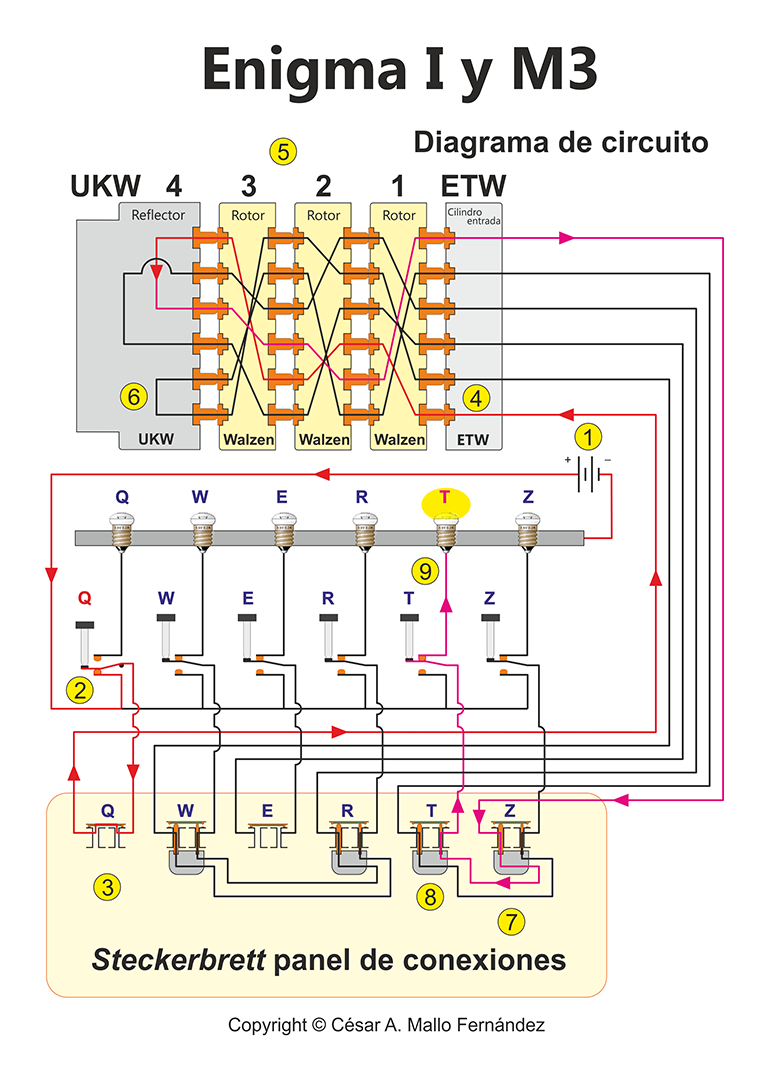
La Enigma era una máquina construida para llevar a cabo permutaciones de letras. Si el operario pulsaba una tecla, la señal eléctrica pasaba a través de diferentes elementos de la máquina, representando cada uno de ellos una permutación. Primero lo hacía por el clavijero, en el que algunas letras eran intercambiadas. La señal eléctrica seguía su camino hasta el cilindro de entrada que es como un rotor fijo, donde se producía una segunda permutación. A continuación, la señal eléctrica entraba en el sistema de rotores, primero en el derecho (o rápido), después en el central y por último en el izquierdo (o lento). Después la señal rebotaba en el reflector e iniciaba su camino de vuelta en orden inverso hasta encender la bombilla correspondiente a la letra cifrada.

Desde un punto de vista meramente formal, podemos representar el camino de la señal eléctrica como el producto de las siguientes permutaciones:

• S: permutación causada por el clavijero o panel Stecker.
• H: permutación causada por el cilindro de entrada.
• N: permutación causada por el rotor derecho.
• M: permutación causada por el rotor central.
• L: permutación causada por el rotor izquierdo.
• R: permutación causada por el reflector.

De izquierda a derecha: Reflector - Rotores - Cilindro de entrada

 

 

De la misma manera, la señal eléctrica en su camino de vuelta, volvía a sufrir nuevas permutaciones, de forma que si por ejemplo el rotor lento (o izquierdo) provocaba una permutación L cuando la señal iba de derecha a izquierda hasta llegar al reflector, dicho rotor introduciría una permutación inversa a L, que denominaremos L⁻¹, en el camino de vuelta de dicha señal cuando va de izquierda a derecha. Del mismo modo, ocurre con el resto de elementos, teniéndo así las permutaciones M⁻¹, N⁻¹, H⁻¹, S⁻¹, que resultan ser las permutaciones inversas de M, N, H y S respectivamente.
Si llamamos I al camino de ida de la señal eléctrica, y V al camino de vuelta de la misma, podremos expresar su recorrido tal y como representa la Tabla 8.

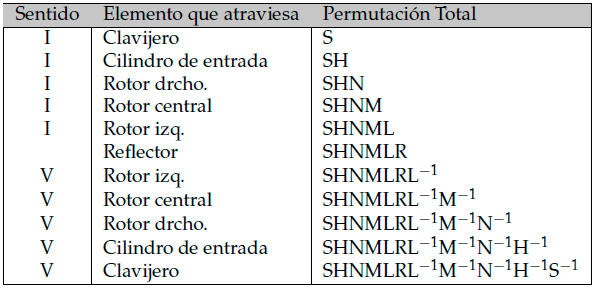
Tabla 8. Permutación total producida.

Por lo tanto, el efecto neto de pulsar una tecla viene representado por la permutación compuesta SHNMLRL⁻¹M⁻¹N⁻¹H⁻¹S⁻¹, o lo que es lo mismo, (SHNML) R (SHNML)⁻¹, es decir cualquier permutación global de Enigma se traduce en una permutación conjugada del reflector.

El reflector era un “medio rotor”. Tenía únicamente 26 contactos en su lado derecho. Internamente, los 26 contactos estaban conectados con cables por parejas, de tal manera que la permutación resultante del reflector consistía en 13 transposiciones disjuntas. Los alemanes utilizaron el mismo tipo de reflector para todos los modelos de la Enigma, el cual era completamente desconocido para los polacos. La permutación provocada por el reflector era la siguiente:

R = (ae)(bj)(cm)(dz)(fl)(gy)(hx)(iv)(kw)(nr)(op)(pu)(st)

De esta manera, como la permutación global de Enigma debe ser del mismo tipo que la provocada por el reflector ya que son conjugadas (ver Teoría de permutaciones más arriba), dicha permutación global puede descomponerse siempre en el producto de 13 transposiciones disjuntas. Sin embargo, se ha de enfatizar el hecho de que cuando el operario pulsaba una tecla, el rotor derecho (o rápido) giraba, y únicamente tras el giro se cerraba el circuito eléctrico. Este hecho llevó a Rejewski a tomar en consideración una nueva permutación que transforma cualquier letra en la siguiente, es decir a → b, b → c, etc. Rejewski denominó a esta permutación P, y es igual a:

P = (abcdefghijklmnopqrstuvwxyz)

que utilizando la notación de ciclos representada anteriormente, significa que “a” se convierte en “b”, “b” se convierte en “c”, y así sucesivamente. Por lo tanto cuando el rotor derecho gira, se tiene que se aplica la permutación P, luego la N y después la inversa de P, es decir PNP⁻¹. Cuando la señal realiza el camino de vuelta, la permutación será justo la inversa, es decir P⁻¹N⁻¹P.

En segundo lugar, a medida que el operario pulsaba por segunda vez una tecla cualquiera, el rotor derecho giraba otra vez, sufriendo la señal entrante la permutación PPNP⁻¹P⁻¹, o lo que es lo mismo P²NP⁻², y la saliente la inversa de ésta, es decir P⁻²N⁻¹P².

También habrá que considerar que cada vez que finalice un ciclo completo el rotor derecho, el central girará una posición, y completado el rotor central su ciclo, entonces girará el rotor izquierdo una posición. Este hecho obliga a considerar dichos movimientos a la hora de formalizar la permutación global. Llegado a este punto, Rejewski se encargó de analizar las relaciones matemáticas de las seis primeras letras cifradas. Si imaginamos los rotores y el clavijero en una disposición concreta, es muy probable que tras pulsar seis teclas, ni el rotor central ni el izquierdo giraran, ya que la probabilidad de que la pulsación de seis teclas hiciera girar el rotor central era de 6/26, mientras que la de que gire el izquierdo es aún muchísimo menor. Por lo tanto no es descabellado considerar esta hipótesis de partida.

Cualquiera que sea la tecla que se pulsara, la señal eléctrica que generaba daba lugar a la siguiente permutación, que denominaremos A:

A = SHPNP⁻¹MLRL⁻¹M⁻¹PN⁻¹P⁻¹H⁻¹S⁻¹ = (SHPNP⁻¹ML) R (SHPNP⁻¹ML)⁻¹      (1)

En una segunda pulsación, el nuevo movimiento del rotor derecho, provocaba que la per- mutación de A fuera alterada. Por lo tanto, la pulsación de una segunda tecla haría que la señal sufriera la permutación B:

B = SHP²NP⁻²MLRL⁻¹M⁻¹P²N⁻¹P⁻²H⁻¹S⁻¹ = (SHP²NP⁻²ML) R (SHP²NP⁻²ML)⁻¹  (2)

Del mismo modo expresaríamos una tercera, cuarta, quinta y sexta pulsaciones, que llamaremos C, D, E y F respectivamente, resultando:

C = SHP³NP⁻³MLRL⁻¹M⁻¹P³N⁻¹P⁻³H⁻¹S⁻¹ = (SHP³NP⁻³ML) R (SHP³NP⁻³ML)⁻¹  (3)

D = SHP⁴NP⁻⁴MLRL⁻¹M⁻¹P⁴N⁻¹P⁻⁴H⁻¹S⁻¹ = (SHP⁴NP⁻⁴ML) R (SHP⁴NP⁻⁴ML)⁻¹  (4)

E = SHP⁵NP⁻⁵MLRL⁻¹M⁻¹P⁵N⁻¹P⁻⁵H⁻¹S⁻¹ = (SHP⁵NP⁻⁵ML) R (SHP⁵NP⁻⁵ML)⁻¹  (5)

F = SHP⁶NP⁻⁶MLRL⁻¹M⁻¹P⁶N⁻¹P⁻⁶H⁻¹S⁻¹ = (SHP⁶NP⁻⁶ML) R (SHP⁶NP⁻⁶ML)⁻¹  (6)

Para poder resolver el sistema de ecuaciones representado por las seis ecuaciones que equivalen a las seis pulsaciones de teclas en Enigma, Rejewski necesitaba conocer N, M, L y R, ya que de este modo podría averiguar la configuración del cableado de los rotores y el reflector. De manera adicional necesitaba conocer S y H, es decir, las permutaciones del clavijero y del cilindro de entrada, ya que estos eran desconocidos. Sin embargo lejos de resultar un sistema compatible determinado, Rejewski partía con el gran handicap de desconocer las permutaciones A, B, C, D, E y F. Para que éstas fueran conocidas, sería necesario conocer el texto llano junto con el cifrado, y las estaciones de radioescucha únicamente proporcionaban el segundo.

Aparentemente las investigaciones de Rejewski se situaban en un callejón sin salida, sin embargo, no estamos ante un personaje común, de ahí la genialidad de sus resultados. En conocimiento de la Enigma comercial, Rejewski basó sus investigaciones en tres resultados fundamentales a la hora de obtener la configuración interna del cableado de los rotores, esto es equivalente a determinar N, M, L y R.

El primer resultado proviene de una propiedad de la máquina Enigma denominada reciprocidad, de tal forma que se puede demostrar que A−¹ = A, B−¹ = B, etc. Esto significa que para una configuración concreta de los diferentes elementos de la máquina Enigma, si pulsamos “s” y obtenemos “r”, también podemos pulsar “r” y obtenemos “s”.

El segundo resultado crucial consistió en aprovechar una de las debilidades ocasionadas por la repetición de las claves. En primer lugar el operador que iba a emitir un mensaje cifrado debía consultar el libro de claves con el fin de obtener la clave maestra (la que iban a utilizar todos los operadores ese día) que representaban la configuración inicial de partida de los rotores. Imaginemos que “sol” es dicha clave maestra. A continuación el operador elegía una “clave de sesión” (También llamada clave del mensaje) para cifrar el mensaje. Imaginemos que dicha clave es “oro”. El proceso entonces era el siguiente:

1. El operador cifraba las letras “oro” con la clave “sol” (es decir, ponía los rotores de forma que en la ventana superior de la máquina apareciera “s-o-l”), obteniendo en el panel luminoso “buu”.
2. Entonces el operador colocaba los rotores en la posición representada por las letras “o-r- o”, y procedía a cifrar el mensaje.
3. El operador enviaba “buu” junto con el mensaje cifrado.

El operador que recibía el mensaje realizaba la operación inversa. Tomaba el libro de claves, colocaba su máquina con los rotores en la posición “s-o-l”, tecleaba “buu” y obtenía en el panel luminoso la clave del mensaje “o-r-o”. Una vez hecho eso, colocaba los rotores en la posición “o-r-o” y tecleaba el mensaje cifrado obteniendo en el panel luminoso el texto plano.

Sin embargo, debido a que los mensajes se transmitían, entre otros medios, por radio, existía la posibilidad de que se produjeran errores de transmisión ocasionados por perturbaciones atmosféricas, además de considerar que en ocasiones se producían errores de transcripción de los operadores. Con el fin de evitar estos posibles fallos, los alemanes establecieron la norma de que la clave del mensaje debía ser cifrada dos veces. Esto es, en el caso que hemos visto, la máquina se ponía en la posición “s-o-l”, y se tecleaba “o-r-o-o-r-o”, obteniéndose “buurqr”. De este modo el receptor del mensaje cifrado recuperaría la clave del mensaje repetida, o de lo contrario, tendría así dos posibilidades para ensayar y obtener el mensaje descrifrado.

El hecho de repetir la clave del mensaje dos veces, significó encontrar un punto de partida para comenzar el ataque a Enigma. Las repeticiones son un filón para los criptoanalistas y Rejewski no dejó pasar inadvertida la sutil relación que existía en el cifrado de la clave del mensaje. Imaginemos que alguien interceptase el mensaje con la clave de mensaje cifrada “buurqr”. Está claro que existe una relación entre las letras primera y cuarta, esto es “b” y “r”. Noso- tros sabemos que equivalen a la letra “o”, pero el criptoanalista sabe que tras pulsar una tecla desconocida (llamémosla “x”) obtiene “b”, y que cuando pulsa en cuarta posición, obtiene “r”. Haciendo uso del lenguaje de permutaciones explicado al principio de esta sección, la permutación A nos indica de qué manera cambian las letras cuando se pulsa una tecla por primera vez, y D lo mismo pero cuando se pulsa una letra por cuarta vez. Esto es equivalente a considerar:

A(x) = b; D(x) = r

El criptoanalista desconoce “x”, pero en virtud de la propiedad recíproca de Enigma, sabe que A(b) = x. Puesto que A transforma “b” en “x”, y D transforma “x” en “r”, la permutación compuesta AD (es decir, la que se obtiene de aplicar A, y después D) nos transforma “b” en “r”:

AD(b) = r

Por lo tanto el criptoanalista desconocía las permutaciones A y D, pero sí que conocía parte de la permutación AD, únicamente considerando el resultado de cifrar la clave del mensaje dos veces (“buurqr”) y establecer la relación entre la primera letra y la cuarta. A lo largo del día se interceptaría una cantidad suficiente de mensajes para establecer más indicativos. Si consideramos los siguientes indicativos de un día dado:

1: (gtaasw)	2: (edjwmv)	3: (ngevjt)	4: (rdjdmv)
5: (cdjqmv)	6: (ntwvso)	7: (dldjbn)	8: (qlaxbw)
9: (zlapbw)	10 (udekmt)	11: (pgjejv)	12: (qtsxsx)

 

donde se puede ver las siguientes relaciones “g” → “a”, “e” → “w”, “n” → “v”, “r” → “d”, . . . En general interceptando unos ochenta mensajes diarios, el criptoanalista podía construirse la siguiente tabla de relaciones:

1ª letra: a b c d e f g h i j k l m n o p q r s t u v w x y z

4ª letra: i r q j w c a y o z f b t v u e x d g h k s m n l p

obteniendo así la permutación completa AD, ordenada por la longitud de sus ciclos:

AD = (aioukfcqxnvsg)(brdjzpewmthyl)

Obsérvese que la permutación resultante se puede descomponer en un número par de ciclos
de idéntica longitud cada pareja. Este hecho no pasó desapercibido para Rejewski, que lo denominó característica.

De igual forma, el criptoanalista podría realizar un análisis idéntico con la segunda y quinta letras de la clave del mensaje cifrado y con la tercera y la sexta, conociendo así las permutaciones compuestas BE y CF respectivamente. No olvide el lector que el fin último de todo este “engendro” es lograr conocer el cableado de los rotores y del reflector, o lo que es lo mismo conocer las permutaciones N, M, L y R.

Veamos cómo llevó a cabo Rejewski esta proeza matemática. Para llegar al fin último antes descrito, tuvo que probar innumerables combinaciones, propiedades, teoremas y leyes. En primer lugar, se construía, gracias a los mensajes interceptados, las permutaciones compuestas AD, BE y CF.

Rejewski centró su atención en el hecho de que la permutación S cambiaba únicamente seis pares de letras, mientras que las restantes catorce letras permanecían invariables. Con el fin de aligerar la notación matemática, denominaremos Q a la permutación producida por el reflector y los rotores central y derecho, es decir Q = MLRL−1M−1. De este modo las permutaciones resultan:

A = SHPNP⁻¹QPN⁻¹P⁻¹H⁻¹S⁻¹

B = SHP²NP⁻²QP²N⁻¹P⁻²H⁻¹S⁻¹

C = SHP³NP⁻³QP³N⁻¹P⁻³H⁻¹S⁻¹

D = SHP⁴NP⁻⁴QP⁴N⁻¹P⁻⁴H⁻¹S⁻¹

E = SHP⁵NP⁻⁵QP⁵N⁻¹P⁻⁵H⁻¹S⁻¹

F = SHP⁶NP⁻⁶QP⁶N⁻¹P⁻⁶H⁻¹S⁻¹

AD = SHPNP⁻¹QPN⁻¹P³NP⁻⁴QP⁴N⁻¹P⁻⁴H⁻¹S⁻¹

BE = SHP²NP⁻²QP²N⁻¹P³NP⁻⁵QP⁵N⁻¹P⁻⁵H⁻¹S⁻¹

CF = SHP³NP⁻³QP³N⁻¹P³NP⁻⁶QP⁶N⁻¹P⁻⁶H⁻¹S⁻¹

Con la representación anterior, Rejewski conocía las permutaciones compuestas AD, BE y CF, y desconocía las permutaciones H, S, N y Q. En un primer intento, consideró que H, es decir la permutación que representa el cilindro de entrada, debiera ser la misma para el modelo militar que para el modelo comercial. Aunque esta suposición resultó ser totalmente errónea, consideremos como punto de partida que la suponemos conocida.

El siguiente paso consistía en determinar A, B, C, D, E y F, considerando únicamente como punto de partida las permutaciones compuestas AD, BE y CF, para lo cual Rejewski utilizó varios teoremas.
Teorema. (Sobre el Producto de Transposiciones) Si dos permutaciones del mismo tipo están factorizadas únicamente como producto de transposiciones disjuntas, entonces su producto contiene un número par de ciclos disjuntos de la misma longitud.

Rejewski argumentó su demostración así:

Si X = (a₁ a₂) (a₃ a₄) (a₅ a₆) . . . (a_2k−3 a_2k−2) (a_2k−1 a_2k),

e Y = (a₂ a₃) (a₄ a₅) (a₆ a₇) . . . (a_2k−2 a_2k−1) (a_2k a₁),

entonces XY = (a₁ a₃ a₅ . . . a_2k−3 a_2k−1) (a_2k a_2k−2 . . . a₆ a₄ a₂).

y continuaba [5, p. 262]:

“Si, de este modo, no hemos agotado todas las letras de la permutación, continuaremos nues tro procedimiento hasta que lo hayamos hecho.”

La composición de permutaciones es una actividad muy común en álgebra abstracta, pero lo que realmente necesitaba Rejewski era factorizar las permutaciones AD, BE y CF.

TEOREMA. (Opuesto al Teorema sobre el Producto de Transposiciones) Si en cualquier permutación de grado par aparecen un número par de ciclos disjuntos de la misma longitud, entonces la permutación puede ser considerada como un producto de dos permutaciones consistentes en transposiciones disjuntas.

Hay que poner de manifiesto que las permutaciones AD, BE y CF satisfacen las condiciones de este teorema. Su demostración es inmediata a partir de lo indicado anteriormente.

Dada XY = (a₁ a₃ a₅ . . . a_2k−3 a_2k−1) (a_2k a_2k−2 a₅ . . . a₆ a₄ a₂),
entonces podemos expresar: X = (a₁ a₂) (a₃ a₄) (a₅ a₆) . . . (a_2k−3 a_2k−2) (a_2k−1 a_2k), e Y = (a₂ a₃) (a₄ a₅) (a₆ a₇) . . . (a_2k−2 a_2k−1) (a_2k a₁)

TEOREMA. Los elementos que forman parte de una única transposición, bien sea de la permutación X, o bien sea de la permutación Y, forman parte siempre de dos ciclos distintos de la permutación compuesta XY.
Teorema. Si dos elementos que se encuentran en dos ciclos diferentes de igual longitud de la permutación XY, pertenecen a la misma transposición, entonces las letras adyacentes a ellas (una por la derecha y la otra por la izquierda) también pertenecen a la misma transposición.

TEOREMA. (SOBRE LAS PERMUTACIONES CONJUGADAS) Si K(i) = j; esto es, K=(...ij...);
entonces T⁻¹KT=(...T(i)T(j)...) Nótese que esto implica que K=(...ij...) y T⁻¹KT=(...T(i)T(j)...) tiene idéntica descomposición en ciclos disjuntos.

Para la demostración, Rejewski consideró que T(T⁻¹KT)(i)=KT(i)=T(K(i))=T(j). En particular, esto significa que la introducción de las permutaciones puede ser ordenada de forma que

K=(......ij......)

T⁻¹KT=(...T(i)T(j)...)

que describe la permutación T.

Con respecto a las permutaciones A, B y C, se podían obtener unas cuantas soluciones (hasta una docena), de las cuales sólo una era la correcta. En este punto, no se podría saber a priori cuál debiera ser la solución correcta. Sin embargo, en ocasiones se interceptaban mensajes trans- mitidos por operarios no demasiado “cuidadosos” que habían cifrado dichos comunicados con claves de mensaje relativamente sencillas del tipo “j-j-j”, “z-z-z”, u otras como “q-w-e”, “b-n-m” que indicaban teclas dispuestas consecutivamente en el teclado de la Enigma. Este hecho podía resultar un punto de apoyo para poder determinar cuál de las soluciones para A, B, y C era la correcta.
En este punto del proceso criptoanalítico, Rejewski no conocía aún siquiera si las ecuaciones que dan A, B, C, D, E, y F resultaban ser despejables para obtener S, N y Q. Podían resolverse en el caso de que el criptoanalista tuviera a su disposición los mensajes de dos días diferentes (en los cuales las conexiones del clavijero fueran diferentes pero los rotores estuvieran en las mismas posiciones), pero el enorme número de distintas posiciones y orientaciones de los rotores hacían de este un problema inviable en la práctica.

Es aquí cuando Rejewski se apoyo en los documentos proporcionados por el espía alemán Hans Thilo Schmidt, que llegaron a sus manos de manera inesperada el 9 de diciembre de 1932. Además de las permutaciones AD, BE, CF (obtenidas mediante radioescucha) y las A, B, C, D, E y F (deducidas por los criptoanalistas polacos), ahora se conocía también la permutación S, y dejaba de ser por lo tanto una incógnita, y consecuentemente resultaba despejable, junto con H (recuerde el lector que hemos partido de la hipótesis de que H es conocida, aunque después se demuestre que no es cierto), resultando:

H⁻¹S⁻¹ASH = PNP⁻¹QPN⁻¹P⁻¹

H⁻¹S⁻¹BSH = P²NP⁻²QP²N⁻¹P⁻²

H⁻¹S⁻¹CSH = P³NP⁻³QP³N⁻¹P⁻³

H⁻¹S⁻¹DSH = P⁴NP⁻⁴QP⁴N⁻¹P⁻⁴

H⁻¹S⁻¹ESH = P⁵NP⁻⁵QP⁵N⁻¹P⁻⁵

H⁻¹S⁻¹FSH = P⁶NP⁻⁶QP⁶N⁻¹P⁻⁶

donde únicamente se tienen las incógnitas N y Q. Rejewski definió las permutaciones U, V, W, X, Y y Z del siguiente modo:

U = P⁻¹H⁻¹S⁻¹ASHP = NP⁻¹QPN⁻¹

V = P⁻¹H⁻¹S⁻¹BSHP = NP⁻²QP²N⁻¹

W = P⁻¹H⁻¹S⁻¹CSHP = NP⁻³QP³N⁻¹

X = P⁻¹H⁻¹S⁻¹DSHP = NP⁻⁴QP⁴N⁻¹

Y = P⁻¹H⁻¹S⁻¹ESHP = NP⁻⁵QP⁵N⁻¹

Z = P⁻¹H⁻¹S⁻¹FSHP = NP⁻⁶QP⁶N⁻¹

A continuación, Rejewski calculó las permutaciones compuestas UV, VW, WX, XY e YZ, resultando:

UV = NP⁻¹[QP⁻¹QP]PN⁻¹

VW = NP⁻²[QP⁻¹QP]P²N⁻¹

WX = NP⁻³[QP⁻¹QP]P³N⁻¹

XY = NP⁻⁴[QP⁻¹QP]P⁴N⁻¹

YZ = NP⁻⁵[QP⁻¹QP]P⁵N⁻¹

Despejó el factor [QP⁻¹QP] de una de las anteriores ecuaciones y lo introdujo en las otras cuatro, obteniendo:

VW = NP⁻¹N⁻¹UVNPN⁻¹

WX = NP⁻¹N⁻¹VWNPN⁻¹

XY = NP⁻¹N⁻¹WXNPN⁻¹

YZ = NP⁻¹N⁻¹XYNPN⁻¹

donde la única incógnita resulta ser la permutación NPN−1. En un día normal, se puede estimar que había del orden de varias decenas de soluciones para VW, WX, XY e YZ, pero lo más importante de todo ello es que estas permutaciones mantenían una estructura común. De no ser así, esto únicamente podía significar dos cosas, bien que se había cometido un error ese día, o bien que ese día en particular el movimiento del rotor lento (situado más a la izquierda) inducía movimiento en el rotor medio para alguna de las posiciones, por lo que era necesario en este caso volver a empezar con otro día. Utilizando el mismo método empleado para obtener A, B, C, D, E y F partiendo de AB, CD, y EF, puede determinarse NPN−1 partiendo de XW, obteniendo varias posibles soluciones. También se pueden obtener distintas soluciones a partir de la ecuación WX, y únicamente existe solución idéntica para las ecuaciones VW y WX. De igual forma, se puede obtener N a partir de NPN−1, para lo cual bastaba aplicar una cualquiera de las 26 posibles permutaciones P que existen para obtener la N, que resultaba ser la permutación inducida por el cableado del rotor que estaba en la posición lenta de ese día.

Sin embargo el lector no debe olvidar que Rejewski supuso erróneamente una hipótesis que luego resultó ser falsa. Consideró que la permutación H era la misma que la de la Enigma comercial: los cables iban de las teclas al cilindro de entrada en el orden del teclado qwert . . . Sin embargo, al probarlo con la Enigma militar, el método no funcionaba. La permutación H era otra. De hecho, los alemanes podían haber incluido en H cualquier permutación que les hubiese dado la gana, y el número de permutaciones distintas con 26 elementos es inmensa. Pero Rejewski logró dar con la clave de este problema a finales de 1932 o principios de 1933, considerando que los alemanes, tan ordenados y metódicos, tal vez hubieran considerado H como la permutación alfabética. Es decir, las teclas se unirían mediante cables al cilindro de entrada siguiendo un orden abcdef . . . Rejewski probó dicha hipótesis, experimentando a buen seguro un sentimiento de triunfo al observar que resultaba ser correcta. De hecho, se comenta que cuando en verano de 1939 los polacos compartieron sus descubrimientos con franceses y británicos en una reunión a las afueras de Varsovia de la que posteriormente hablaremos, la primera pregunta del reputado criptólogo británico Dillwyn Knox a Rejewski fue: “¿cuál es la permutación del cilindro de entrada?”. Al escuchar la trivialidad de la respuesta, parece que Knox montó en cólera por no haber considerado una posibilidad tan obvia.

 

3.4 3ª Etapa. La amenaza de la invasión y la búsqueda de aliados

Rejewski repitió el mismo proceso con las relaciones que existían entre los caracteres 2º y 5º, y los 3º y 6º de la clave de los mensajes. En este punto, llegó a la conclusión que estas cadenas de caracteres eran una consecuencia directa de la configuración y disposición de los rotores y que el clavijero influía únicamente en que las letras cambiaban, es decir variaban las permutaciones, pero la estructura cíclica de éstas permanecía invariable aún cuando la configuración del clavijero cambiara. Por lo tanto el número de ciclos y sus longitudes dependía única y exclusivamente del orden en el que estaban dispuestos los rotores y de su configuración inicial de partida. Rejewski denominó característica a este número de ciclos y longitudes. El número de características que los polacos tenían que estudiar se reducía por lo tanto drásticamente de 1016 a 105.456, o lo que es lo mismo 6 × 26 × 26 × 26, que siendo aún un número grande, sí que permitía abordar manualmente el ataque al código de Enigma. Con respecto a las características, Rejewski comentaba [19, p. 217]:

“Esta estructura es la más característica, y aunque su representación difiere cada día, su rasgo es siempre el mismo: en cada línea los ciclos de idéntica longitud aparecen siempre por parejas. Observando el papel que dicha estructura jugaba, la denominé estructura característica, o simplemente la característica de un día determinado.”

Rejewski pasó algo más de un año recopilando lo que denominó catálogo de características, y gracias a sus descubrimientos, los polacos fueron capaces de construir un catálogo para cada configuración de rotores. Con la ayuda del libro de claves proporcionado por Schmidt, se pudo llevar a cabo con éxito la tarea de desencriptación. Schmidt había proporcionado los libros con las claves de septiembre y octubre (es decir de dos trimestres diferentes), lo que permitió deducir la configuración de dos rotores. Bastaba esperar hasta el comienzo del año 1933, para que los polacos pudieran obtener la configuración del tercer rotor y deducir así la del reflector. A últimos de enero de 1933, el código de la Enigma había sido descubierto.

Tras el incendio del Reichstag a últimos de febrero de 1933, y con la subida al poder de lo que después se convertiría en el régimen nazi, los polacos del BS4, a petición de Rejeski, consideraron oportuno reforzar las tareas criptológicas, por lo que la plantilla se aumentó a 6 operarios de descifrado, entre ellos Jerzy Rózycki y Henry Zygalski, los cuales habían sido minuciosamente entrenados con anterioridad.

Con el fin de mecanizar la tarea de encontrar el catálogo adecuado para una configuración determinada, los polacos construyeron unas réplicas de la Enigma militar. Antoni Palluth, Edward Fokczyński, y los hermanos Ludomir y Leonard Danilewicz, ingenieros y directores de la compañia de Radiomanufactura AVA, encargada de surtir al Biuro Szyfrów todo tipo de material tecnológico para comunicaciones, acometieron la fabricación de dichas réplicas de Enigma que se construyeron casi artesanalmente durante la noche para mantener el asunto en completo secreto. Un operario de total confianza llevaba a cabo el ensamblaje mecánico de dicha máquina. AVA que había sido fundada en 1929 y tenía sus oficinas centrales en el número 34 de la calle Nowy Swiat en Varsovia, recibió el encargo de la comandancia general polaca para llevar a cabo la construcción de 15 de estas réplicas a principios de febrero de 1933, y concluyó la entrega de dicho encargo a mediados de 1934.

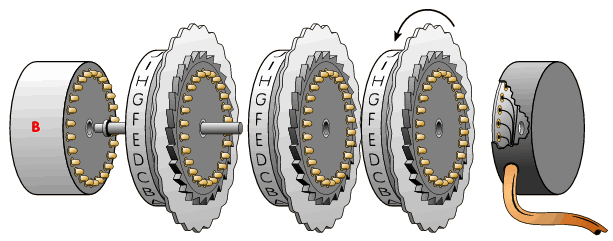
Durante los primeros meses de la primera victoria polaca sobre Enigma, los operarios tenían que obtener la configuración inicial de manera prácticamente manual, de forma que giraban los rotores metálicos con 17.576 posibilidades, habiendo 263 posibles configuraciones. Esta tarea resultaba, además de tediosa, profundamente dolorosa puesto que los dedos de los criptólogos llegaban a sangrar, ya que no era posible que éstos delegaran dicha actividad en el personal técnico. Fue entonces cuando Rejewski, con ayuda de Antoni Palluth, inventó el “ciclómetro”, un mecanismo que permitió manejar a los criptólogos polacos un catálogo de 105.456 características. El ciclómetro era una máquina Enigma doble (con seis ruedas y dos reflectores) pero en la que el segundo juego de ruedas se ajustaba automáticamente tres posiciones con respecto al primero. El efecto que se conseguía es el mismo que si se pulsase una tecla en una máquina convencional, es decir, se teclean otras dos y luego se teclea la misma otra vez, únicamente que con el ciclómetro sólo era necesario teclear una vez, en lugar de cuatro. Durante tres años las comunicaciones encriptadas con Enigma resultaron ser un libro abierto para los polacos. Sin embargo, para su desgracia, el 1 de noviembre de 1937, los alemanes cambiaron el reflector de las máquinas, lo que significó tener que reconstruir nuevamente el catálogo.

En enero de 1938, la comandancia general polaca llevó a cabo una investigación interna con el fin de cuantificar la eficacia del trabajo del BS4. Los resultados del estudio realizado durante dos semanas fueron bastante concluyentes, ya que ponían de manifiesto que el equipo formado por diez individuos (entre criptólogos y operadores) era capaz de descifrar alrededor del 75 % de todos los mensajes interceptados, lo que daba una idea del éxito de los polacos, considerando que parte de los mensajes interceptados resultaban en ocasiones ilegibles o incompletos debido a las interferencias.

Para desdicha de los polacos, el 15 de septiembre de 1938 los alemanes volvieron a dar una vuelta de tuerca con el fin de buscar la optimización de la Enigma. Esta vez los cambios introducidos dejaron inservibles por completo todos los métodos de desencriptación llevados a cabo hasta el momento. Dichos cambios consistían básicamente en que tanto la configuración de los rotores, como las claves de cada mensaje eran elegidas libremente por el operador en cuestión. Las tres letras de la clave se transmitían de forma abierta en la cabecera del mensaje y éstas precedían a las seis letras que resultaban del doble cifrado de la clave del mensaje. Por ejemplo, la cabecera “FDA GHRMER” indicaba que la configuración de los rotores era FDA (con el orden de los rotores establecido previamente en los libros por el alto mando nazi, y que en aquel momento cambiaba todos los días), y las otras seis letras correspondían al cifrado doble de la clave del mensaje. Todo el resto del proceso no sufrió ningún cambio significativo adicional, aunque cabe destacar que por entonces, el número de conexiones del Stecker estaba entre cinco y ocho, y que la configuración del Ringtellung se cambiaba todos los días.

El Ciclómetro

Figura 19. Diseño del Ciclómetro

Con el fin de automatizar la tarea de confeccionar el catálogo de características, Rejewski y los polacos del BS4 construyeron el ciclómetro. La Figura 19 muestra una reproducción de dicho aparato realizada a partir de un diseño original del propio Rejewski. Este aparato estaba formado por dos bancos de rotores interconectados entre sí, de forma que el de la derecha iba desplazado tres posiciones con respecto al de la izquierda. Bajo dichos bancos de rotores estaban el panel de lámparas y las palancas, una por cada letra del alfabeto. Cuando una de estas palancas era accionada, una corriente eléctrica atravesaba varias veces ambos bancos de rotores y entonces se encendía un número par de lámparas, que eran las correspondientes a los dos ciclos asociados a la permutación AD. Entonces, accionando otra palanca de una letra no iluminada, se deducían dos ciclos asociados. De este modo se determinaba la descomposición en ciclos disjuntos de AD. Si se variaban entonces el orden de los rotores y sus posiciones iniciales, se calculaban todas las permutaciones AD existentes. Con todo esto, los polacos del BS4 elaboraban el catálogo, ya que las permutaciones BE y CF asociadas a una posición determinada de los rotores coincidían con la AD, sólo que bastaba adelantar los rotores de la derecha del ciclómetro una o dos posiciones respectivamente.

Los cambios introducidos se traducían en una modificación de la configuración de los rotores en cada uno de los mensajes, lo cual a su vez provocaba la modificación de los productos AD, BE y CF, sin embargo, los alemanes continuaban cometiendo el mismo error, que consistía en repetir la clave del mensaje al inicio de cada comunicación. Los polacos aprovecharon esta pequeña debilidad. Con el fin de elaborar el catálogo de características, calcularon 105.456 productos posibles de AD. Pudieron comprobar que el 40 % de estas permutaciones contenían ciclos de longitud 1, y del mismo modo ocurría con los productos BE y CF. Pongamos un ejemplo, supongamos que tenemos tres mensajes interceptados con las siguientes cabeceras:

FDE BWHBXT                QSC GJVBJM                ZDR WSXTGX

Como podemos observar subrayado se produce la repetición en idénticas posiciones de algunos caracteres. Los británicos acuñarían el término female para referirse a dichas repeticiones. El mensaje con la cabecera FDE BWHBXT, indica que la permutación AD correspondiente contiene el ciclo (B). Utilizando la terminología introducida por los británicos, dicha cabecera se expresaba como una 1,4-female. Del mismo modo, en el segundo mensaje con la cabecera QSC GJVBJM, tendríamos una 2,5-female y (J) es un ciclo de la permutación BE, y en el tercer mensaje con la cabecera ZDR WSXTGX tendríamos una 3,6-female y (X) es un ciclo de CF.

Recordemos que las conexiones del Stecker no tenían ninguna influencia en las longitudes de las permutaciones AD, BE y CF, ya que dichas longitudes dependían única y directamente del orden de los rotores y de sus posiciones iniciales, viniendo determinadas por las diferencias entre las letras del Grundstellung y las del Ringstellung (ver 2.3). Por un lado, el Grundstellung era distinto en cada uno de los mensajes, aunque conocido, sin embargo, el Ringstellung era el mismo en todos los mensajes de un mismo día, aunque desconocido. El objetivo fundamental del trabajo criptológico consistía fundamentalmente en identificar correctamente el orden de cada uno de los rotores y la configuración del anillo de entre las 105.456 posibles configuraciones. Sorprendentemente, este enorme número de posibilidades se reducía en un factor de 0,4 cada vez que aparecía un ciclo de longitud 1, ya que únicamente el 40 % de las permutaciones AD (o bien las BE, o las CF) presentaban este tipo de ciclos unitarios. Si las permutaciones AD, BE y CF eran elegidas de manera aleatoria, la teoría de probabilidades arrojaba un resultado sorprendente, y es que el 11,5 % de las cabeceras de los mensajes presentaban females. De este modo, se necesitaban únicamente doce o trece females entre un centenar de mensajes interceptados para determinar de manera unívoca el orden de los rotores y el Ringstellung.

De forma adicional al trabajo desarrollado por Rejewski, en septiembre de 1938 Zygalski inventó un ingenioso método que proporcionaría a los polacos la posibilidad de descifrar de manera masiva los mensajes cifrados interceptados, ya que determinaba el orden de los rotores y el Ringstellung. El método de las hojas de Zygalski o Netz (del alemán Netzverfahren, “método neto”), rudimentario aunque bastante efectivo, basaba su fundamentación en la aparición de females. Zygalski preparó 6 paquetes de 26 hojas cada uno, donde cada paquete representaba una posible configuración de los rotores (cada uno de los 6 órdenes posibles de los rotores y cada una de las 26 posiciones del rotor izquierdo). En cada una de las hojas se escribía una letra y a continuación se dibujaba una cuadrícula de 51×51 (60×60 cms aprox.) en la que se rotulaban tanto las abscisas como las ordenadas con todas las letras, comenzando por la esquina superior izquierda. Las letras horizontales representan las posiciones del rotor central y las verticales las del derecho, de modo que cada pequeño cuadrado, representaba una permutación con ciclos de una letra correspondiente a esa posición de los rotores, es decir una female. Los cuadrados correspondientes a las 1,4-females se perforaban directamente. Sin embargo las 2,5 y 3,6-females, necesitaban un proceso de “normalización” que consistía básicamente en adelantar su Grundstellung derecho una o dos posiciones respectivamente. Utilizando el ejemplo presentado anteriormente:

QSC GJVBJM ⇒ QTC GJVBJM                   ZDR WSXTGX ⇒ ZDT WSXTGX

Realizada la nombrada normalización, se procedía a repetir el proceso para cada orden de los rotores y cada posición del Ringstellung del rotor izquierdo. Fijado el orden de los rotores, se normalizaban de nuevo aquellas females cuyo Grundstellung se tradujera en un avance del rotor central. Pongamos un ejemplo, imaginemos que el orden de los rotores era II-I-III, y que el Grundstellung era SGV. Dicho Grundstellung debía ser normalizado a SHV, ya que la V es la letra que provoca en el rotor III un avance del rotor situado inmediatamente a su izquierda, en este caso el rotor central en el que se encuentra el I. Acto seguido, se seleccionaban el juego de 26 hojas asociadas al orden de rotores establecido, y fijada una letra del Ringstellung del rotor izquierdo, pongamos por ejemplo la letra F, se consideraba el Grundstellung de una primera female. Supongamos que una 1,4-female era RDW. Como R − F = M, se escogía la hoja correspondiente a la letra M que servía de patrón básico con el que comenzar a trabajar, y se colocaba sobre una mesa transparente iluminada por debajo. A continuación se tomaba otra 1,4-female, pongamos por ejemplo MYS. Como M − F = H, se seleccionaba la hoja correspondiente a H y se colocaba sobre el patrón básico representado por la letra M, pero desplazada 5 pequeños recuadros hacia la derecha (ya que de la Y a la D van 5 letras), y 4 pequeños recuadros hacia abajo (porque de la S a la W van 4 letras). Se repetía la operación con el resto de females, y una vez colocadas todas las hojas se observaba si la luz de la iluminación que había debajo de la mesa transparente traspasaba algún agujero común a todas ellas. Si se habían conseguido una cantidad suficiente de females, el haz de luz atravesaba un único agujero, el cual proporcionaba de manera inmediata el orden de los rotores y el Ringstellung del rotor izquierdo. Con el fin de obtener el de los otros dos rotores, es necesario observar que, fijada una de las females (normalizada si ha sido necesario), las letras del agujero de la hoja correspondiente determinaban la posición de los rotores que la había producido. Dicha posición era precisamente la diferencia entre el Grundstellung de la female y el Ringstellung que se pretendía obtener. Por consiguiente, el Ringstellung de los rotores central y derecho se obtenía restando al Grundstellung de una female las letras del agujero. Como última operación quedaba obtener las conexiones del Stecker. Recordemos que el Stecker no cambiaba la estructura de ciclos, sino que únicamente alteraba las letras de los mismos, en este caso los de longitud 1 del catálogo de características por las letras repetidas de las females, entonces la letra repetida de una female estaba conectaba con una de las letras de los ciclos de longitud 1 de la correspondiente permutación AD del catálogo. Contemplando todas las females a un tiempo, no era difícil averiguar cual.

Pero, ¿qué ocurría si el haz de luz atravesaba más de un agujero? En ese caso se procedía a realizar las anteriores operaciones con cada uno de ellos, y las contradicciones descartaban casi todos los casos, permitiendo considerar la solución correcta como aquella que permitía descifrar los mensajes.

Figura 20. Hojas de Zygalski en el Museo de Bletchley Park.

Por otro lado, también Jerzy Rózycki contribuyó en gran medida a la lucha contra Enigma desarrollando el denominado método del reloj, que hacía posible determinar en ocasiones cuál de los rotores estaba en la posición del rotor derecho o rápido. Su método fue más tarde perfeccionado en Bletchley Park por Alan Turing, desarrollando la técnica denominada bamburismo. Hasta finales de 1935, los alemanes cambiaban el orden de los rotores sólo una vez cada tres meses, por lo que hasta entonces obtener la disposición del rotor rápido no resultaba de tan vital importancia. Sin embargo, a partir del 1 de febrero de 1936, dicho cambio se empezó hacer cada mes, y el 1 de noviembre de ese año comenzó a hacerse cada día, de ahí la importancia de obtener la disposición del rotor rápido. Veamos un ejemplo para ver en qué consistía dicho ingenioso método. Imaginemos que tenemos dos textos en alemán y los ponemos uno debajo del otro letra a letra como muestra la Tabla 9.

Tabla 9. Ejemplo de textos en alemán.

W E M G O T T W I L L R E C H T E G U N S T   . . . 
D E R A L T E L A N D M A N N A N S E I N E N  . . .

Se puede observar que de media existirá una probabilidad de coincidencia de letras en ambos textos de 2/23. Debemos esperar que esta característica se repita con textos cifrados mediante una clave idéntica. Sin embargo si se encripta cada texto utilizando una clave distinta (en este caso se utilizaron las claves O-G-P y J-N-C, con las conexiones E/G, J/Y, S/O, en el Stecker) resultan los mensajes cifrados que se muestran en la Tabla 10.

Tabla10.TextoscifradosconEnigma.

V D Z T H D B G H X S P V Y E C G F I A D H    . . .
F B X G G P A X H W X U O F M Q H U U B Z K O  . . .

La Tabla 10 muestra que en este caso, la probabilidad de que coincidan letras en la misma posición en los dos textos cifrados con claves diferentes es de 1/23. Este hecho se debe a la distinta frecuencia de aparición de las letras en idioma alemán. En un lapso de 23 letras este hecho no ocurrirá demasiadas veces. Si por el contrario se tuvieran dos mensajes de 260 letras de longitud, con este método se podría generalmente diferenciar si los dos mensajes se cifraron con idéntica clave o con diferentes. Para ello teniendo disponible una cantidad suficiente de material cifrado, normalmente se podía encontrar una docena de pares de mensajes tales que en cada pareja las primeras dos letras de las claves eran idénticas, mientras que las terceras letras eran diferentes. Entonces, se escribían ambos mensajes uno encima de otro. Existían dos posibles formas de escribir un mensaje encima de otro, dependiendo de en qué posición de partida se encontrara el rotor rápido una vez que se producía el desplazamiento del rotor medio. Estas posiciones eran conocidas y diferentes para cada uno de los tres rotores. Por ejemplo, si el rotor I estaba colocado en la posición del rotor rápido, entonces el desplazamiento del rotor medio ocurría cuando el rotor rápido se desplazaba de la letra Q a la R. Si el rotor II estaba situado en la posición del rotor rápido, el desplazamiento sucedía cuando se desplazaba de la letra E a la F, y si el rotor III se situaba en la posición del rotor rápido, el desplazamiento sucedía cuando se desplazaba de la V a la W. Para cada una de las dos formas de escribir los mensajes, era suficiente contar el número de columnas con idénticas letras para determinar cuál era el modo correcto de escribir los mensajes y por lo tanto determinar cuál de los tres rotores estaba localizado en la posición del rotor rápido. De todos los métodos criptológicos desarrollados por el BS4, el método del reloj era el único que tomaba en consideración las características propias del lenguaje alemán, esto es, la frecuencia de aparición de las letras de su alfabeto.

La lucha constante entre la optimización de los recursos polacos y los cambios sucesivos realizados en la Enigma militar por parte de los alemanes, significó desarrollar no una única técnica, sino varios métodos que permitieran desentrañar el código de Enigma de la mejor manera posible. Además de las hojas de Zygalski o el método del reloj de Rózycki, hubo otros como el método ANX. Los polacos utilizaron un hecho bastante llamativo, y es que el texto en claro de muchos mensajes alemanes interceptados comenzaban por “ANX” (“AN” significa PARA en alemán y la “X” se empleaba como separador de palabras). Una vez que era determinada la posición inicial del rotor derecho en un mensaje que comenzara por “ANX”, la de los otros dos rotores se podía obtener mediante la utilización del catálogo de características construido por Rejewski.

Con la ayuda de unas invenciones basadas en las réplicas de Enigma, Rejewski fue capaz de encontrar la clave del día de las comunicaciones alemanas antes de que acabara el día. Dichas invenciones, denominadas bombas, resultaron ser unos aparatos electro-mecánicos basados en la combinación de 6 réplicas de la Enigma polaca construida previamente, y tenían como principal objetivo mecanizar su sistema de catalogación de modo que pudieran encontrar las posiciones correctas de los rotores. La máquina era capaz de probar 17.576 combinaciones diferentes en un tiempo aproximado de dos horas. Debido a las seis disposiciones posibles de rotores, era necesario tener seis de las máquinas de Rejewski trabajando en paralelo: cada una de ellas representaba una de las posibles disposiciones. Ahora, con cada mensaje interceptado, se desarrollaba una tabla de relaciones para encontrar las cadenas resultantes, y con éstas se acudía al catálogo, encontrando la disposición de los rotores de la clave del día. Quedaba por resolver el problema del clavijero, así que Rejewski ingenió un método para obtener la configuración de éste: una vez conocida la disposición de los rotores, quitaba todos los cables y comenzaba a teclear el texto del mensaje. Al operar de este modo se obtenían frases sin sentido, puesto que se desconocía las conexiones del clavijero, pero de vez en cuando se obtenía un texto parecido a: “VULAR A MURICH”. Se deducía fácilmente que esto querría decir “VOLAR A MUNICH”, con lo que se veía que la U y la O estaban intercambiadas así como la R y la N. Con un número considerable de mensajes cifrados interceptados, era perfectamente posible deducir todas las posiciones del clavijero. Enigma había sido vencida nuevamente.

Veamos un ejemplo de la operatividad de las bombas. A veces entre las females interceptadas, había tres de ellas que presentaban la repetición de una misma letra.

TGB FGTFAC                 VHJ DFMNFX                 ZGP FMSFNQ

La primera de estas females pone de manifiesto que el ciclo (F) se encuentra presente en la permutación AD. Imaginemos que la letra F no se viera alterada por el Stecker, es decir la F no está conectada a ninguna otra letra a través de una conexión de clavija. Entonces el ciclo (R) también aparece en la sustitución AD que se obtendría sin ninguna conexión en el Stecker. Tenemos ya conocimiento de que el número de tales productos AD es 105.456, tantos como posibles configuraciones de los rotores (orden y posiciones iniciales). De todos estos productos, desconocemos cuantos contienen al ciclo (F), sin embargo teniendo como aliado a la Teoría de Probabilidades, sabemos que fijado un ciclo de longitud 1, si A y D se eligen aleatoriamente entre las de su clase, entonces el 4 % de los productos AD contienen dicho ciclo, lo cual reduce drásticamente el anterior número de 105.456 en un factor de 0,04 cada vez que se observe una female con la letra F repetida. Como en nuestro ejemplo, 105.456 ·(0, 04)3 = 6, 75, existirán seis o siete configuraciones de rotores que ocasionen las tres females representadas en el ejemplo. Las máquinas ingeniadas por Rejewski eran las encargadas de automatizar la identificación de dichas configuraciones.

Desde el punto de vista de su diseño, la bomba consistía en tres ciclómetros conectados convenientemente. Un motor eléctrico permitía a los seis bancos de rotores girar de forma sincronizada recorriendo las 17.576 posiciones posibles. En el momento en el que se alcanzaba una posición en la que los tres ciclómetros reconocían el ciclo programado, (F) en el ejemplo expuesto, el mecanismo se detenía mostrando dicha posición.

Los polacos construyeron seis bombas, una por cada orden de los rotores. Previamente a su utilización, era preciso ajustar adecuadamente las posiciones de los rotores de los ciclómetros. Para ello, en primer lugar se normalizaban las females del mismo modo que se realizaba en las hojas de Zygalski. Entonces, se asociaba cada uno de los tres ciclómetros a una female y se colocaban sus rotores en la posición indicada en el Grundstellung, con el rotor derecho del segundo banco desplazado tres posiciones respecto a su homónimo del primer banco. En el ejemplo expuesto, el primer banco se colocaría en la posición “TGB”, el segundo en la posición “TGE”. Después de colocar los rotores se activaba la palanca de la letra F y el mecanismo de la bomba se accionaba. Las seis bombas encontraban las seis o siete posiciones que ocasionaban las tres females en unas dos horas. Entre esas posiciones se encontraba la que proporcionaba la clave, que para conocerla se seguía el mismo procedimiento que con los agujeros de las hojas de Zygalski.

Las bombas mecanizaron enormemente el proceso criptoanalítico, eliminando en gran parte los posibles errores debidos al factor humano. Sin embargo, su principal inconveniente era que se necesitaban al menos tres females con la misma letra repetida y que además dicha letra permaneciera invariante por el Stecker, algo que no ocurría todos los días.

Una vez que tenía la clave del día poseía la misma información que el receptor a quien iba dirigido el mensaje y, por tanto, podía descifrar los mensajes con la misma facilidad. Los polacos interceptaron multitud de mensajes alemanes, con lo cual si no evitaban el peligro de invasión por parte de éstos, sí que podían ofrecer una idea de las pretensiones que el Tercer Reich tenía con respecto a Polonia.

Figura 21. Bomba criptológica

 

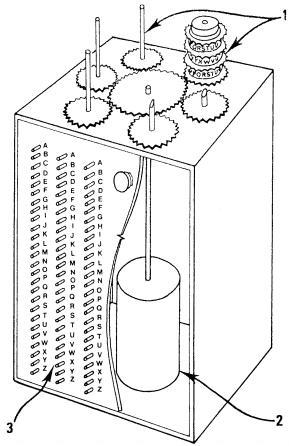
Diseño original de Rejewski. 1. Rotores, 2. Motor eléctrico, 3. Interruptores (Cortesía de Janina Sylwestrzak, hija de Rejewski). Este concepto fue posteriormente desarrollado por los miembros del Servicio de Inteligencia Británica (SIS) en Bletchley Park. Se trataba de una invención más desarrollada que el ciclómetro. Según parece su nombre fue acuñado debido al sonido “tic-tac” que éstas emitían cuando probaban las distintas posiciones de los rotores. Otra versión afirma que a Rejewski le vino la inspiración de las máquinas cuando estaba en una cafetería comiendo una bomba, un helado con forma de hemisferio. Las bombas mecanizaron eficazmente el proceso de descifrado. Significaba una respuesta natural a la Enigma, que era una mecanización de la codificación.

La inteligencia polaca, mantuvo constantemente informado a su gobierno a través del trabajo realizado por el BS4, lo que les hizo poner sobre aviso a la opinión internacional de las pretensiones invasoras de Hitler para con Polonia. Muy a su pesar, los aliados no tomaron en demasiada consideración estos avisos. Además los acontecimientos no hacían más que empeorar la maltrecha situación de los polacos ya que el 15 diciembre de 1938, los militares nazis, conscientes del origen comercial de Enigma, consideraron oportuno suministrar a los operadores de comunicaciones dos nuevos rotores además de los 3 rotores con los que ya contaba la máquina, lo cual aumentaba enormemente el rango de disposiciones de los mismos, exactamente a la enorme cantidad de 1, 59 × 1020. En lugar de tener 6 disposiciones distintas de los rotores, ahora se tenían 60, lo cual significaba para los polacos tener que construir 54 máquinas nuevas para poder hacer frente a este nuevo reto, que de tenerlas (opción esta ni remotamente probable ya que no tenían presupuesto para ello) aumentaría el tiempo de obtención de las claves en gran medida. Del mismo modo, ahora eran necesarias 26 · 54 = 1404 nuevas hojas de Zygalski. Además, el 1 de enero de 1939, los alemanes aumentaron el número de cableado del Stecker hasta 10, provocando un efecto devastador en las labores criptoanalíticas polacas. El método criptológico de Rejewski quedaba prácticamente anulado, de forma que tan sólo uno de cada diez días eran capaces de descifrar los mensajes alemanes. Sin embargo, los polacos contaron esta vez con la accidental “ayuda” del servicio de inteligencia del partido nazi para ser capaces de obtener el cableado interno de los nuevos rotores. Parece ser que la red de comunicaciones nazi incorporó los dos nuevos rotores, pero continuaba cifrando sus mensajes con el sistema previo al 15 de septiembre. Gracias a este desliz, pudieron obtenerse las conexiones de los nuevos rotores sin más que manipulando el antiguo sistema de ecuaciones fundamentado por Rejewski.

A pesar de obtener el cableado interno de los nuevos rotores, la capacidad de cálculo de la pequeña oficina polaca se veía completamente desbordada, y encima el 1 de enero de 1939 el método de las bombas de Rejewski quedaba totalmente inoperante ya que los alemanes incrementaron hasta diez el número de conexiones del Stecker. Todo este cúmulo de acontecimientos dejó a los polacos en una situación de aislamiento ciertamente preocupante lo cual les condujo inexorablemente a buscar ayuda. Sin demasiadas alternativas, la inteligencia polaca no tuvo más remedio que recurrir a sus aliados franceses, con la esperanza de que sus mayores recursos les permitieran aprovechar los avances polacos y sacar un mayor partido al concepto de la bomba. Enigma recuperaba virtualmente su inviolabilidad.

 

Reunión del bosque de Pyry

Hasta 1937, la sección alemana de la Oficina de cifrado, BS-4, se había alojado en el edificio del Estado Mayor polaco, el majestuoso Palacio Sajón del siglo XVIII, en Varsovia. Ese año la BS-4 se mudó a nuevas instalaciones especialmente construidas en el Bosque de Kabacki cerca de Pyry, al sur de Varsovia. Allí, las condiciones de trabajo eran incomparablemente mejores que en los espacios reducidos del edificio del Estado Mayor.

El 25 y 26 de julio de 1939, los polacos invitaron a Gustave Bertrand, el comandante de la inteligencia francesa que ya les había proporcionado los documentos de H. T. Schmidt, para que éste conociera el nuevo centro en Pyry, en los bosques de Kabacki, unos diez kilómetros al sur de Varsovia, cuyo nombre en clave era “Wicher” (Vendaval), donde además le mostrarían los logros conseguidos por el BS4.

Para conocer mejor esta reunión, vea en Biuro Szyfrów la reunión del Bosque de Kabacki en Pyri y continúe con el regalo a los aliados.

Una instalación de la oficina polaca de cifras en los años treinta, en Lasy Kabacki, cerca de Varsovia

Véase también

• Historia de las máquinas de cifrado Enigma
• Biuro Szyfrów
• Universidad Adam Mickiewicz de Poznań
• Pc Bruno
• Cadix
• Bletchley Park
• Ultra
• Bombe
• Las máquinas de cifrado Enigma
• Principio de funcionamiento y detalles técnicos - Enigma
• Hans Thilo Schmidt
• Biografías de criptógrafos y matemáticos
• Biografías militar - político
• Historia de la criptografía
• Criptografía

Principal

Evolución de la criptografía

Siguiente

4. Bletchley Park