1. Breve evolución histórica de la criptología hasta la 2ª Guerra Mundial
Ult. rev. 14-05-2024
A lo largo de la historia, el hombre ha sentido la necesidad de codificar sus mensajes con la mera intención de que estos pasaran inadvertidos a los ojos de curiosos y mantener intacto el secretismo de los mismos. Surgieron así los primeros mensajes ocultos primitivos que rápidamente encontraron un nicho de utilidad en aquellas comunicaciones cuya privacidad debía ser garantizada. A esta comunicación secreta lograda mediante la ocultación se la denomina esteganografía, derivada del steganos o “encubierto” y graphein o “escribir”. La principal desventaja de esta ciencia era que cualquiera podría interceptar un mensaje oculto y comprometer la seguridad de la comunicación.
Paralelamente a la esteganografía, surgió la ciencia de la criptografía, del griego kryptos o “escondido”, cuya finalidad consistía más que en ocultar el mensaje, ocultar su significado mediante un proceso de codificación. De forma añadida surgieron las primeras técnicas de análisis cuya finalidad principal consistía en desenmascarar el contenido secreto de los mensajes cifrados, lo que se denominó criptoanálisis. La evolución de las técnicas criptográficas supuso el avance y desarrollo de nuevas técnicas de análisis críptico.
Desde su inicio, la criptografía encontró su principal utilidad en el arte de la guerra. Algunos de los testimonios más antiguos que narran la utilización de escrituras secretas se remontan a Herodoto que escribió una crónica acerca de los conflictos entre Grecia y Persia en el siglo V a.C. Gracias a la mera ocultación de un mensaje de aviso del griego Demarato que vivía en la ciudad persa de Susa, donde se revelaban los planes estratégicos de invasión del archipiélago heleno del líder persa Jerjes, Grecia tomó una clara ventaja y pudo hacerse con la victoria y evitar la invasión en el año 480 a.C.
Los métodos criptográficos se pueden clasificar en métodos de encriptación simétricos y asimétricos. En los primeros se utiliza la misma clave para cifrar y descifrar los mensajes encriptados, al contrario que los segundos que utilizan diferentes claves. Los métodos asimétricos nacieron a finales del siglo XX y revolucionaron la ciencia de la criptografía. Dentro de los métodos simétricos de cifrado podemos encontrar los métodos de sustitución y transposición.

Índice:
1.1. Métodos de Sustitución
El primer ejemplo documentado de un método de sustitución de encriptación fue utilizado por Julio César en La guerra de las Galias, para enviar un mensaje a Cicerón que estaba sitiado y a punto de rendirse, sustituyendo las letras romanas por griegas haciendo ininteligible el mensaje. Para cifrar un mensaje mediante el Cifrado de César, cada letra de dicho mensaje era reemplazada con la letra de tres posiciones después en el abecedario. Por tanto, la A sería reemplazada por la D, la B por la E, la C por la F, y así sucesivamente. Por último la X, la Y y la Z serían reemplazadas por la A, la B y la C respectivamente. De ahí, que por ejemplo, “ATACAR” se cifraría como “DWDFDU”. César rotaba el abecedario de tres en tres letras pero en general funcionaba con cualquier número acordado entre el emisor y el receptor del mensaje.
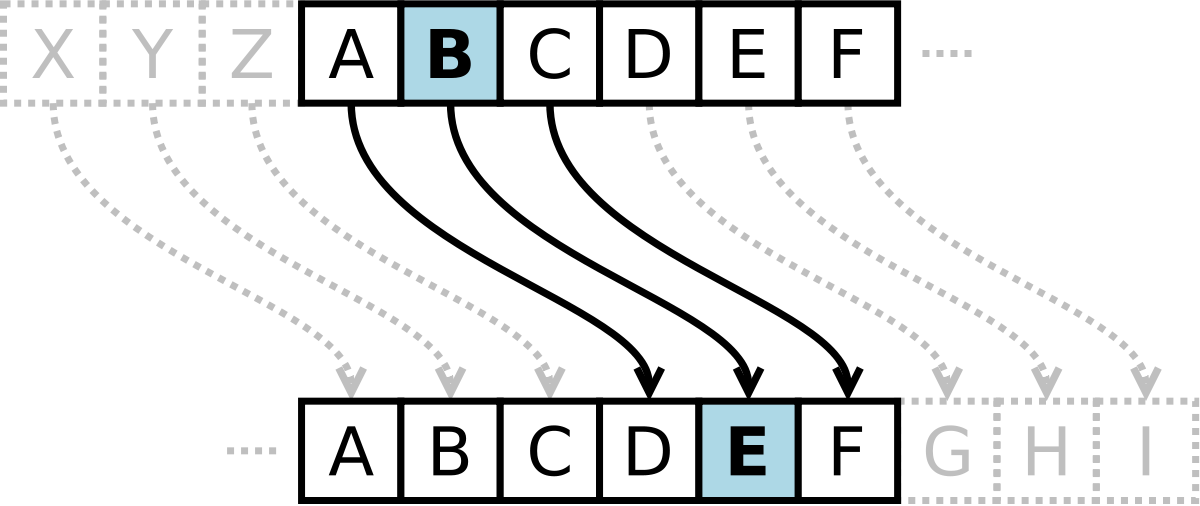

Figura 2. Sello conmemorativo sirio de Al Kind˜ı (1994)
Durante siglos este tipo de cifrado monoalfabético se consideró prácticamente imposible de romper, sin embargo con el paso del tiempo surgieron las técnicas de análisis criptográfico nacidas en el seno de la civilización musulmana. Aunque no se conoce el autor originario de la técnica de análisis de tablas de frecuencia, parece que al final del siglo IX d.C., Abu Yusuf Ya’qub ibn Ishaq Al-Kindi (801-873), conocido como el filósofo de los árabes, fue el primero en documentar dicho análisis en su libro Sobre el descifrado de mensajes criptográficos descubierto de forma casual en el Archivo de Estambul en 1987. Al-Kindi que trabajó en filosofía, astrología, astronomía, cosmología, química, lógica, matemática, música, medicina, física, psicología y meteorología, manifestaba en dos breves párrafos:
“Una manera de resolver un mensaje cifrado, si sabemos en qué lengua está escrito, es encontrar un texto llano diferente escrito en la misma lengua y que sea lo suficientemente largo para llenar alrededor de una hoja, y luego contar cuántas veces aparece cada letra. A la letra que aparece con más frecuencia la llamamos «primera», a la siguiente en frecuencia la llamamos «segunda», a la siguiente «tercera», y así sucesivamente, hasta que hayamos cubierto todas las letras que aparecen en la muestra de texto llano.
Luego observamos el texto cifrado que queremos resolver y clasificamos sus símbolos de la misma manera. Encontramos el símbolo que aparece con más frecuencia y lo sustituimos con la forma de la letra «primera» de la muestra de texto llano, el siguiente símbolo más corriente lo sustituimos por la forma de la letra «segunda», y el siguiente en frecuencia lo cambiamos por la forma de la letra «tercera», y así sucesivamente, hasta que hayamos cubierto todos los símbolos del criptograma que queremos resolver.”
La técnica de Al-Kindi consiste en examinar un fragmento extenso de texto normal, o quizás varios, para establecer la frecuencia de cada letra del alfabeto. En castellano, dicha frecuencia se ve representada por la Tabla 1. A continuación, es necesario examinar el texto cifrado y determinar la frecuencia de cada letra. Si la letra más corriente en el texto cifrado es, por ejemplo, la J, entonces parecería probable que sustituyera a la E (que es la más comúnmente utilizada en español). Y si la segunda letra más frecuente en el texto cifrado es la P, probablemente sustituya a la A, y así sucesivamente. La técnica de Al-Kindi, conocida como análisis de frecuencia, muestra que no es necesario revisar cada una de las billones de claves potenciales. En lugar de ello, es posible revelar el contenido de un mensaje codificado analizando simplemente la frecuencia de los caracteres en el texto cifrado, y realizando una comparativa con la tabla de frecuencias de un texto en el idioma considerado.
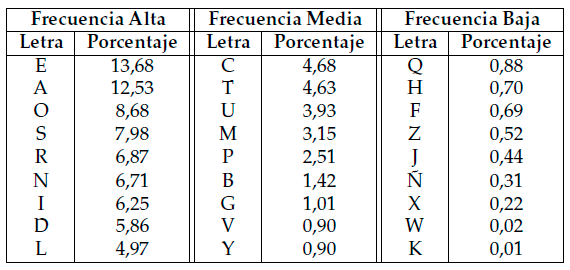
Tabla1. Frecuencias de caracteres en castellano
1.2. Métodos de Transposición
Tras el análisis de frecuencia, la criptografía continuó su avance surgiendo entonces nuevos métodos simétricos de encriptación cada vez más y más sofisticados, denominados Métodos de Transposición, que consisten como su definición indica en transponer los textos, es decir que ahora no son las letras las que cambian, sino su orden.
Pongamos un ejemplo; imaginemos que tanto el emisor del lenguaje cifrado como el receptor consideran en principio un número menor de nueve dígitos como clave, por ejemplo el 2313. Dicha clave ponía de manifiesto que el texto debía ser escrito en tres columnas (en principio sin considerar espacios entre palabras). De este modo el emisor codificaría la frase “DESEMBARCAR AL AMANECER”.
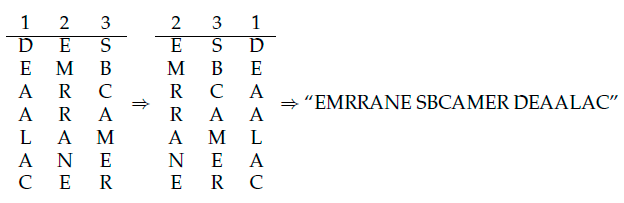
De esta forma el receptor recibía dicho mensaje y colocaba dicho grupo de letras en tres columnas, de modo que el primer grupo de letras correspondía con la segunda columna del lenguaje original, el segundo se correspondía con la tercera columna, y el tercer grupo se correspondía con la primera columna.
1.3. El Disco de Alberti
Durante siglos, la cifra de sustitución monoalfabética simple había resultado lo suficientemente complicada para garantizar su indescifrabilidad. Sin embargo las técnicas de análisis de frecuencias desarrolladas por Al-Kindi fueron rápidamente transmitidas al mundo occidental, comprometiendo seriamente la integridad de los mensajes cifrados. Comenzaba a ser evidente que la batalla entre los criptógrafos y los criptoanalistas estaba comenzando a ser ganada por el segundo grupo. Es así cuando en torno a 1460, el erudito renacentista natural de Florencia, Leon Battista Alberti (1404-1472) comenzó a trabajar en una nueva técnica de cifrado de mensajes. Mientras gozaba de una conversación durante un paseo por el Vaticano, su amigo, y a la sazón secretario pontificio, Leonardo Dato, puso al corriente a Alberti de los últimos adelantos en cuanto a criptografía se refería. Esta conversación fortuita animó a Alberti a investigar, llegando a la conclusión de que era necesario utilizar dos o más alfabetos cifrados, alternando entre ellos durante la codificación con el fin de fortalecer la encriptación y confundir así a los potenciales criptoanalistas.
De 1466 a 1467 escribió su tratado De Componendis Cyphris, considerado como el escrito sobre criptología más antiguo del mundo occidental. En dicho tratado explica el desarrollo de las técnicas polialfabéticas. A partir de ahí, Alberti analiza diversos procedimientos: sustituciones de tipos diferentes, transposiciones de letras dentro de palabras y mensajes obtenidos marcándose las posiciones de ciertas letras en un texto inocente. Finalmente concluye su introducción con la descripción de su invención, el disco cifrante, también conocido como Disco de Alberti.

Figura 3. Estatua de Leon Battista Alberti en la Galería Uffizi, Florencia
“Fijo dos discos en una placa de cobre. Uno, el mayor, será fijo y el otro, el menor, movible. El diámetro del disco fijo es superior en un noveno al del disco móvil. Divido la circunferencia de cualquiera de los dos en veinticuatro partes iguales llamadas sectores. En cada uno de los sectores del disco grande escribo en orden alfabético normal una letra mayúscula roja: primero A, a continuación B, después C, etc, omitiendo H y K que no son indispensables.”
De este modo, Alberti obtuvo un total de 20 letras, pues J, U, W e Y tampoco figuraban en su alfabeto. En los cuatro sectores restantes escribió los números 1, 2, 3 y 4. Haciendo referencia a los veinticuatro sectores del disco pequeño escribió:
“. . . una letra minúscula, en negro, no en la orden normal como en el disco fijo, pero en una orden incoherente. De esta forma, se puede suponer que la primera letra será a, la décima segunda g, la décima tercera q y así sucesivamente, de modo que todos los veinticuatro sectores sean llenados porque el alfabeto latino posee veinticuatro caracteres, siendo el vigésimo cuarto &. Efectuados estos arreglos, se coloca el disco pequeño sobre el grande, de modo que una aguja pasada por los dos centros sirva como un eje común alrededor del cual girará el disco móvil.”
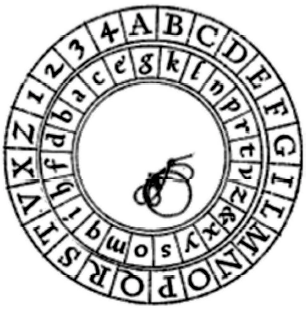
Disco de Alberti (imagen del manuscrito original “De Componendis Cyphris”, 1466)
Se considera una de las letras del disco móvil como letra llave o letra índice, por ejemplo k. Hecho esto el emisor alinea esta letra llave con cualquier letra del disco externo e informa de la posición del disco móvil al receptor escribiendo la letra escogida. Alberti usó el ejemplo de k alineada con B.
“Usando este punto de partida, cada letra del mensaje representará la letra fija por encima de ella. Después de escribir tres o cuatro letras, puedo cambiar la posición de la letra-índice de modo que k esté, por ejemplo, sobre D. Después, en mi mensaje, escribiré una D mayúscula y, a partir de este punto, k no significará más B y sí D, y todas las letras del disco fijo tendrán nuevas letras equivalentes.”
1.4. La Cifra Vigenère
Alberti puede ser considerado como el inventor del cifrado polialfabético y sus estudios sirvieron de base para trabajos posteriores como los de Johannes Trithemius que inventó la tábula recta, Giovanni Porta y sobre todo del diplomático francés de mediados del siglo XVI Blaise Vigenére (1523-1596), que a diferencia de Alberti utilizó la enorme cantidad de 26 alfabetos cifrados. Vigenère utilizó como base la tábula recta de Trithemius, y la amplió generando la tábula de Vigenère, que se muestra en la Tabla 2.
Figura 4. En la imagen siguiente: Blaise de Vigenère Bovrbonois (1515)


Tabla 2. Tábla de Cifrado Vigenère
Desde el punto de vista de su funcionamiento, se numeran las 26 letras del abecedario de forma que A = 0, B = 1, . . . , Z = 25. En términos matemáticos puede expresarse como:
Yi = (Xi + Zi) mod T
donde T representa el número total de letras del alfabeto considerado (en general 26), Xi representa el ordinal de las letras de la palabra clave considerando las filas de la Tabla 2, es decir, que a P le corresponde al numero 15 en modo horizontal, y Zi representa el ordinal de la letra de texto plano (sin cifrar) considerada, que se corresponde con las columnas de la Tabla 2, esto es, la L en modo vertical le corresponde al numero 11. Finalmente Yi representa el ordinal de la letra cifrada en el alfabeto considerado. Entonces la ecuación quedará de la siguiente manera Yi = (15 + 11) mod 26. El resultado es 0, donde 0 es igual a A en modo horizontal. Haciendo uso de la Tabla 2, vamos a ilustrar cómo el emisor generaba un mensaje cifrado y el receptor descifraba dicho mensaje utilizando una codificación-descodificación por medio de una palabra clave. Imaginemos que el emisor quiere cifrar la orden “movilizar las tropas dos km al sur” considerando como clave la palabra “norte”. La palabra “norte” especifica que se utilizará la codificación de los alfabetos 13, 14, 17, 19 y 4 en ese orden hasta finalizar el texto llano original. De este modo el emisor haría uso de la Tabla 2 y para la primera letra del mensaje original “m” se corresponde en el alfabeto 13 con la “Z”, la segunda letra “o” se corresponde en el alfabeto 14 con la “C”, la “v” se corresponde en el alfabeto 17 con la “M”, la “i” se corresponde en el alfabeto 19 con la “B”, y la “l” se corresponde en el alfabeto 4 con la “P”, a partir de aquí el emisor continuaría con el proceso de encriptación volviendo a hacer uso de la secuencia de alfabetos 13, 14, 17, 19 y 4, y así sucesivamente. Con todo lo anterior el mensaje cifrado tendría el aspecto especificado en la Tabla 3.

Tabla 3. Encriptación de mensaje mediante el Cifrado de Vigenère (I).
El receptor del mensaje cifrado podría invertir el proceso de encriptado repitiendo la operación en la Tabla 2, entrando primero en el alfabeto 13 y mirando en el alfabeto llano que la “Z” se corresponde con la “m”, la “C” del alfabeto 14 se corresponde en el alfabeto llano con la “o”, y así sucesivamente.
Este sistema de cifrado tenía dos ventajas fundamentales respecto a los sistemas de encriptación conocidos hasta ese momento. La primera era que aparentemente resultaba inexpugnable al análisis de frecuencias, ya que una misma letra no tenía porqué repetir un patrón de repetición, y aparecía cifrada con diferentes letras. La segunda era la enorme combinación de posibilidades a barajar. Todas estas ventajas tendrían que haber sido suficientes para que todos los secretarios de cifra de Europa hubieran adoptado este método como sistema oficial de encriptación, sin embargo esta cifra, a todas luces perfecta, permanecería prácticamente ignorada durante los dos siglos y medio posteriores, seguramente debido a la complejidad de su aplicación a nivel práctico, que supondría tener que realizar un gran esfuerzo tanto a emisores como a receptores de mensajes cifrados con dicho método.
Durante algo más de doscientos cincuenta años, la Cifra Vigenère fue considerada prácticamente impenetrable, sin embargo la aparición en escena en la primera mitad del siglo XIX de la excéntrica figura del inglés Charles Babbage (1791-1871) como el principal protagonista del criptoanálisis de la época supuso un punto de inflexión. Babbage, entre otras cosas, es considerado como uno de los precursores de la que hoy consideramos una de las herramientas cotidianas más importantes como es el ordenador. Babbage se interesó por la desencriptación desde que era muy joven. En una ocasión, recordó cómo esa afición de su infancia le había proporcionado en ocasiones más de un quebradero de cabeza:
“Los chicos mayores hacían cifras, pero si yo conseguía unas pocas palabras, generalmente descubría la clave. En ocasiones, la consecuencia de este ingenio resultó dolorosa: los dueños de las cifras detectadas a veces me daban una paliza, a pesar de que la culpa la tenía su propia estupidez.”
Estas palizas no le desanimaron, al contrario, sirvieron de acicate para continuar cautivado por el criptoanálisis. En su autobiografía escribió “. . . descifrar es, en mi opinión, una de las artes más fascinantes”.
El interés de Babbage por la Cifra Vigenère se había producido en cierto modo de una manera fortuita, gracias a la intervención de un dentista de Bristol aficionado a la criptografía llamado John Hall Brock Thwaites. Resulta que en 1854, Thwaites afirmó haber inventado una nueva cifra, que en su desconocimiento de la Cifra Vigenère, resultaba similar a ésta, y escribió sobre sus avances en el Journal of Society of Arts, con la firme intención de patentar su descu- brimiento. Babbage escribió a esa sociedad poniendo de manifiesto que Thwaites llegaba con varios siglos de retraso manifestando “la cifra . . . es muy antigua, y aparece en multitud de libros”. En lugar de retractarse Thwaites adoptó una posición desafiante y no pidió ningún tipo de disculpas instando a Babbage a que aceptara el reto de descifrar una de las cifras generadas con su idea. Descifrable o no, no tenía relación alguna con el hecho de que fuera o no nueva, pero este nuevo reto despertó la curiosidad de Babbage que se embarcó en la búsqueda de un punto débil en la Cifra Vigenère.
¿Pero cómo fue capaz Babbage de desencriptar una cifra supuestamente indescifrable? Pongamos un ejemplo para comprender el proceso. Imaginemos que nuestra palabra clave es “SUR”, y que el mensaje que queremos encriptar es “El adulto y el joven en el espejo”. Nuestro mensaje se encriptaría haciendo uso de los alfabetos cifrados 18, 20 y 17, repitiendo este ciclo hasta concluir el mensaje. En la Tabla 4 podemos observar que los tres determinantes “el” del texto llano original, se repiten en el mensaje cifrado. Esto es porque sus letras ocupan las posiciones 1-2, 10-11 y 19-20, es decir cada determinante está separado 9 posiciones del otro, que resulta múltiplo de la palabra clave “SUR” que es de 3 letras. Estas repeticiones no pasaron desapercibidas para Babbage y le proporcionaron un punto de partida desde el que comenzar a romper la Cifra Vigenère.

Tabla 4. Encriptación de mensaje mediante el Cifrado de Vigenère (II)
La brillante técnica empleada por Babbage consistía en una especie de estudio de frecuencias pero adaptada a la particularidad de la Cifra Vigenère. Imaginemos que se ha interceptado el mensaje de la Tabla 5, del cual únicamente se sabe que ha sido encriptado con la Cifra Vigenère, pero del que se desconoce la palabra clave utilizada.
La primera fase del ataque al código llevada a cabo por Babbage, consistió en buscar secuencias de letras que aparecieran más de una vez en el texto, esto es buscar patrones de repetición de caracteres, y una vez encontrado alguno ver la distancia de separación entre uno y otro para ver la multiplicidad de dicha distancia y de este modo establecer una hipótesis sobre la longitud de la palabra clave.
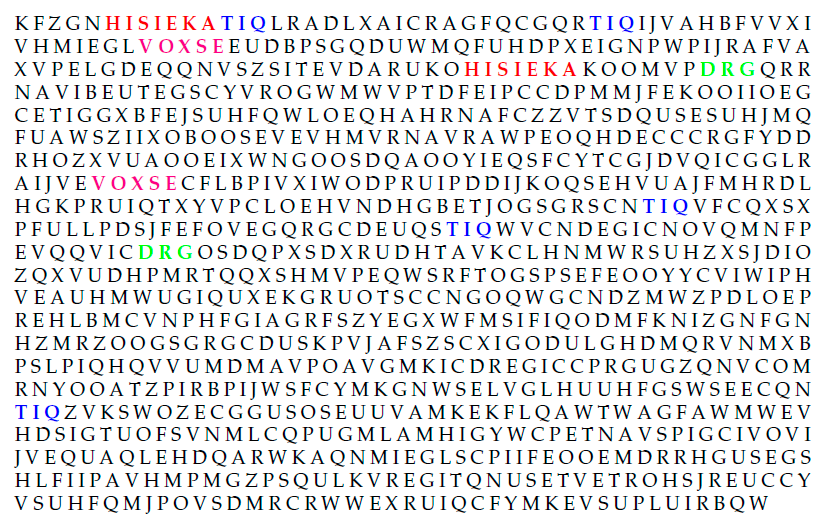
Tabla 5. Texto cifrado interceptado con patrones de repetición resaltados
Analizando el texto cifrado, se procedería a construir una tabla de observación de patrones de repetición de caracteres, y la separación entre ellos, donde se representa la multiplicidad de esta separación (Tabla 6).

Tabla 6. Patrones de repetición de caracteres y espaciado entre ellos
Aunque todavía no se tenga demasiada información sobre el mensaje cifrado, tras enumerar qué secuencias se repiten, así como los espacios que hay entre las repeticiones, el resto de la Tabla 6 trata de identificar los factores de los espaciamientos: la división entera de estos espaciamientos. Por ejemplo, la secuencia HISIEKA se repite tras 112 letras, por lo que los números 2, 4, 7, 8, 14 y 16 son factores, ya que pueden dividir exactamente a 112 sin dejar decimales. Parece lógico considerar que la palabra clave tiene una longitud de 7 caracteres, ya que este factor se repite en todas las secuencias. En principio no conocemos aún la palabra clave con la que el mensaje ha sido cifrado, por lo que consideraremos que se trata de la palabra X1-X2-X3-X4- X5-X6-X7. Cada una de estas letras proporciona un alfabeto de cifrado, de forma que el cifrado polialfabético puede ser considerado como una combinación de 7 cifrados monoalfabéticos responsables cada uno de ellos de un séptimo de la codificación del total del mensaje. Luego las letras 1ª, 8ª, 15ª, 22ª, . . . , estarán codificadas por el alfabeto cifrado correspondiente a X1. Parece evidente que conocer la palabra clave tanto para el emisor como para el receptor es una fase crucial en el desencriptado del texto llano original. Llegado a este punto podemos recurrir al análisis de frecuencias monoalfabético ya visto anteriormente. Para ello se lleva a cabo en el texto cifrado un “conteo” de las frecuencias de aparición de cada uno de los caracteres del alfabeto correspondiente al carácter X1 (Figura 6).
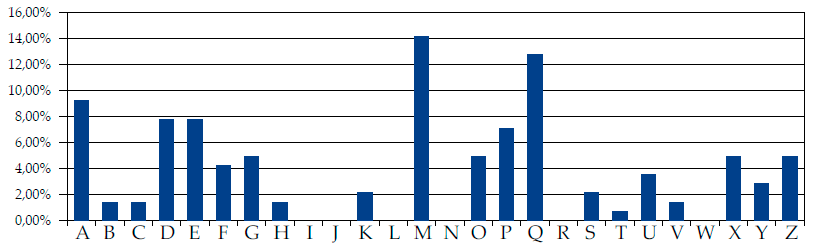
Figura 6. Distribución de frecuencias para las letras del texto cifrado, codificado utilizando el alfabeto cifrado X1 (porcentaje de apariciones)
En este punto ha de recordarse que cada alfabeto cifrado del cuadro Vigenère es simplemente un alfabeto normal desplazado entre 1 y 26 posiciones. Por esta razón, la distribución de frecuencias de la Figura 6 debería tener rasgos similares a la distribución de frecuencias de un alfabeto normal, excepto que habrá sido desplazado unas cuantas posiciones.
Si se realiza una comparativa gráfica de las Figuras 6 y 7, ambas debieran superponerse aunque con un desplazamiento, ya que recordemos que los alfabetos cifrados de la Tábula de Vigenère son generados por el desplazamiento de varios caracteres con respecto al alfabeto llano original. Fijándonos en los patrones más representativos podemos ver que los bloques “MNOPQ”, “XYZA” y “DEFGH” del alfabeto cifrado, se corresponden respectivamente con los bloques “ABCDE”, “LMNO” y “RSTUV” del alfabeto llano. De este modo podemos considerar que el alfabeto llano se corresponde con el alfabeto cifrado identificado por la letra “M”, es decir el número 12.
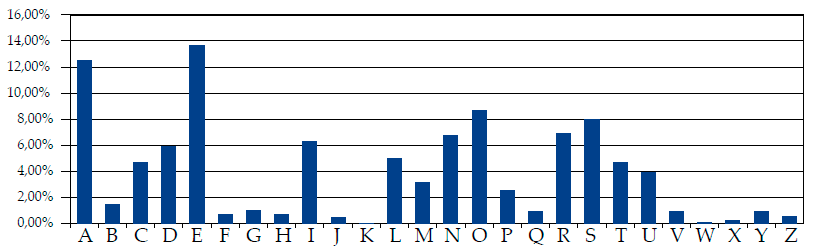
Figura 7. Distribución de frecuencias de caracteres para el idioma castellano
Identificado este primer alfabeto, procederíamos del mismo modo con el resto de caracteres de la palabra clave, esto es X2, X3, . . . , actividad que proponemos al lector como juego de entrenamiento. Llegaríamos a la conclusión de que el texto cifrado interceptado puede encriptarse-desencriptarse con la palabra clave “MERCADO”. Descubierta la palabra clave el resto es una tarea relativamente sencilla.

Tabla 7. Texto original desencriptado (de la novela de Alejandro Dumas “El Conde de Montecristo”)
Es muy probable que la técnica de criptoanálisis de la cifra Vigenère realizado por Babbage se realizara en torno a 1854, poco después de su altercado con Thwaites, sin embargo su descubrimiento no tuvo ningún tipo de repercusión ya que nunca publicó sus logros. El descubrimiento no se conoció hasta 1920, cuando gran parte de los trabajos de Babbage fueron examinados por un grupo de investigadores. De forma paralela pero independiente, el oficial retirado del ejército prusiano Friedrich Wilhelm Kasiski (1805-1881) desarrolló una técnica criptográfica similar a la de Babbage, que publicó en 1863 en “Die Geheimschriften und die Dechijfrirkunst” (“La escritura secreta y el arte del desciframiento”), y que hoy día es conocida como la Prueba Kasiski. Según algunos historiadores, es posible que Babbage, aparte de que tenía el hábito de no finalizar la mayoría de proyectos en los que se embarcaba, no publicara sus descubrimientos debido a presiones recibidas por parte de la inteligencia británica, ya que la guerra de Crimea había estallado recientemente, lo que hace muy probable que los británicos quisieran gozar de una ventaja sobre sus enemigos rusos, obligando a Babbage a mantener su secreto.

