6. Las máquinas Lorenz

Ult. rev. 01-02-2023

Índice

6.1 Características y particularidades
6.2. El algoritmo de codificación
6.3. Criptoanálisis y desencriptado
Véase también

6.1 Características y particularidades

Muy a pesar del ingenio que supuso la ruptura del código de la Enigma, no fue ésta la máquina que inspiró el nacimiento de lo que hoy día podemos considerar (aunque con algunas restricciones) como el primer ordenador de la historia. Durante el curso de la Segunda Guerra Mundial, Alan Turing fue el encargado de romper el difícil código naval alemán (llamado Shark), lo que sirvió para que los aliados se hicieran finalmente con la victoria. Sin embargo, Enigma sólo significó la mitad de la historia de la lucha criptológica contra los alemanes.

Máquina Lorenz SZ42

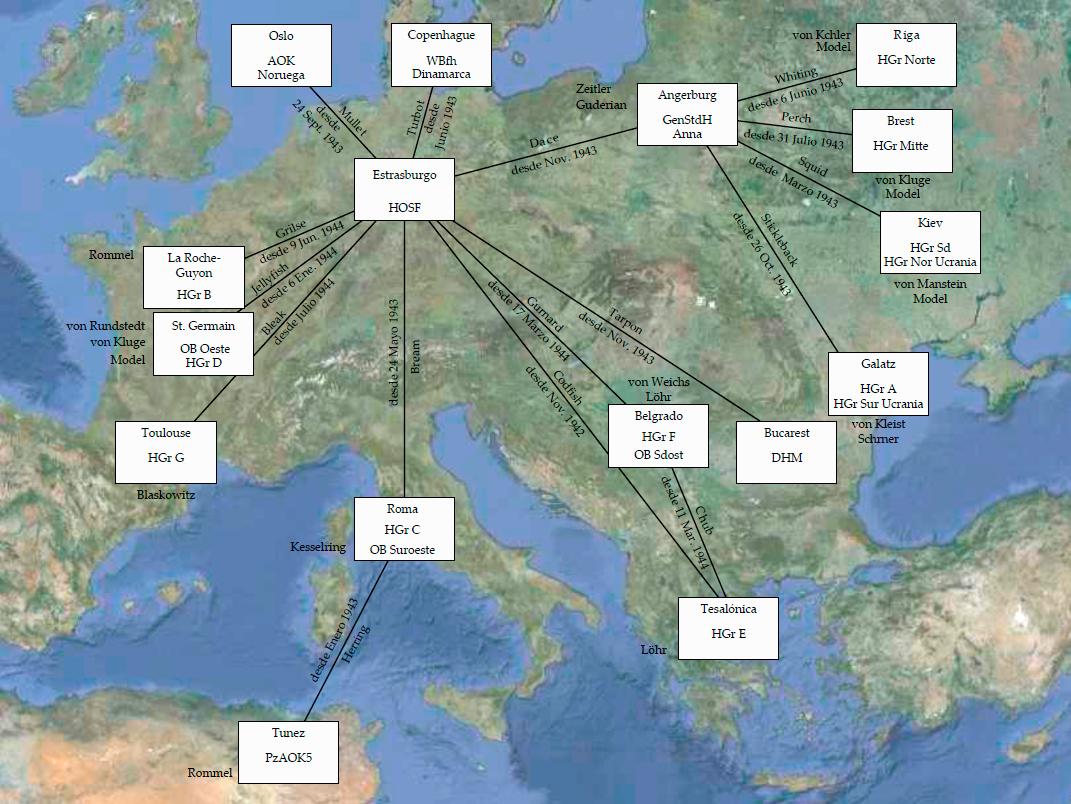
En 1940, a principios de la guerra, los británicos interceptaron unas señales de teletipo en las que no se utilizaba el código Morse. Su “música” era completamente distinta al sonido característico proveniente de las Enigma. Se trataban de señales cifradas con las llamadas máquinas Lorenz SZ40 y SZ42 (Schlüsselzusatz, que significa “cifrado adjunto”) que estaban conectadas a un teletipo. Mientras que la Enigma se usaba generalmente por unidades de combate, las Lorenz fueron utilizadas para las comunicaciones cifradas entre el propio Hitler y su alto mando. Esto es debido a que la cúpula del ejército nazi consideraban que las Lorenz ofrecían si cabe una mayor seguridad que las Enigma ya que utilizaban 12 rotores. En cierto modo las Lorenz sirvieron para “dictar” el curso de la guerra. En Bletchley Park, los criptoanalistas organizaban su trabajo clasificándolo dependiendo de los códigos o claves con los que se referían a las distintas redes de comunicación utilizadas por los alemanes. El tráfico de las señales alemanas que circulaban a través de teletipo eran etiquetadas con la clave Fish (pez), y a su vez las que provenían de las máquinas Lorenz, se etiquetaron como Tunny (atún). La siguiente imagen muestra las lineas de teletipo interceptadas y rotas por los aliados.

Líneas de teletipo interceptadas durante la 2ª Guerra Mundial. Los cuadros representan el destino de la línea de teletipo con el código de identificación alemán y el/los general/es al mando del destacamento nazi situado en ese destino. Se puede observar el nombre clave de las líneas como se conocían en Bletchley (todas con nombres de peces), y la fecha en la que se consiguió romper el código de encriptación por primera vez.

Equipos de operarios de Enigma (Cortesía de Helge Fykse)

Si hiciéramos una comparativa con respecto a las Enigma, además de su mayor potencia de encriptación, las Lorenz tenían una ventaja muy clara con respecto a éstas. Mientras Enigma necesitaba en su operativa un mínimo de tres individuos tanto en el lugar de emisión como en el de recepción, esto es, un operador que tecleaba el mensaje con un ayudante que anotaba las letras a medida que éstas se encendían en la máquina, que finalmente proporcionaba a un operador de radio que emitía en código morse el mensaje cifrado. Del mismo modo se repetía un proceso similar pero al revés en el lugar de recepción del mensaje. Sin embargo, las Lorenz únicamente necesitaban un operador en el lugar de emisión y otro en el de recepción con el consiguiente ahorro de personal y por lo tanto un mayor aprovechamiento y optimización de los recursos humanos.

6.2. El algoritmo de codificación

Cada vez que se escribía un carácter desde el teclado éste era transformado mediante el Código Baudot (1).

Un carácter es representado por una secuencia de 5 bits, esto es, por una secuencia en binario compuesta de 5 dígitos, que en Bletchley Park se representaba mediante puntos y cruces (o 0 y 1 en binario). El método utilizado por la máquina Lorenz para encriptar un mensaje consistía en generar una secuencia aleatoria de 5 números binarios o bits y operar por parejas de bits, uno procedente de la letra a codificar y el otro de la secuencia aleatoria, de acuerdo con el operador booleano XOR al que también se conoce como exclusivo OR. La máquina en cuestión disponía de un total de 12 ruedas denominadas pinwheels con las que se generaba la secuencia aleatoria de 5 bits. De estas ruedas, cinco recibían el nombre de “chi” o χ y giraban paso a paso de modo regular, otras cinco llamadas “psi” o ψ giraban paso a paso de modo irregular, y finalmente había dos ruedas motoras, denominadas µ₁ y µ₂.

Imaginemos que se quiere codificar la letra M que en código Baudot resulta · · ××× (en binario: 00111) [23]. Los pasos a seguir son los siguientes:

El operador configura las ruedas χ con la posición inicial de los pines que equivalen a off-on-on-off-on, lo que significa que se invierten los valores de la codificación (puntos por cruces y cruces por puntos -en binario 0 por 1 y 1 por 0-) en aquellos dígitos correspondientes a la posición on. De esta manera · · ××× (00111) se convierte en · × · × · (01010).

En segunda instancia se aplica la suma aritmética en módulo 2 (similar a la aplicación del operador booleano XOR) a las parejas de bits procedentes de las secuencias que representan la letra M y la letra M modificada por las ruedas χ. Esta operación es de tal forma que si los dos bits son iguales el resultado es · (esto es × + × = · , o bien · + · = · ), y si son distintos, el resultado es × (esto es × + · = × , o bien · + × = ×) (2). En este caso, tenemos

· · ××× + · × · × · = · ×× · ×
cuyo resultado es equivalente a 01101 en binario.

En tercer lugar el operador configura las ruedas ψ con la posición inicial de los pines que equivalen a on-off-on-off-on de modo que
· ×× · × ⇒ ×× · · ·
Por último se suman los dos últimos caracteres obtenidos, esto es
· ×× · × + ×× · · · = · × · × ·
equivalente a 01010 en binario, secuencia que en el código Baudot corresponde a la letra R, es decir resumiendo, la letra M se ha codificado como la letra R

1. Código Baudot es un código inventado en 1874 parecido al ASCII de los ordenadores actuales, pero utilizado en telegrafía. El código original, conocido como Alfabeto Internacional de Telégrafía Número 1, dejó de utilizarse en 1901, ya que en su lugar apareció un código modificado por Donald Murray, donde se reordenaban algunos caracteres, propiciado por el desarrollo de un teclado parecido al de una máquina de escribir. Entonces la disposición de los bits fue disociada de las teclas del operador. Murray arregló su código de modo que los caracteres más usados produzcan la menor cantidad de cambios de estado, lo que reducía al mínimo el desgaste en el equipo. La Western Union desarrolló una nueva modificación del código de Murray. Esta modificación final supuso la supresión de algunos caracteres, y es la que se conoce generalmente como el Código Baudot, también conocido como Alfabeto Internacional de Telegrafía Nº2 (ITA2). El ITA2 todavía se utiliza en teléfonos para sordos, en radioaficionados, y en RTTY (radioteletipo).

2. Esta operación “aritmética” fue inventada por un empleado de la división de desarrollo de la ATT llamado Gilbert S. Vernam, para permitir la aplicación intensiva en el teletipo del cifrado descrito durante la 1ª Guerra Mundial.
Esta suma no era una suma convencional, sino la aplicación de una de las aritméticas binarias descritas por Boole, en particular la del operador.

6.3. Criptoanálisis y desencriptado

La historia de la desencriptación del código de las máquinas Lorenz, resulta cuanto menos un tanto rocambolesca. Según parece el 30 de agosto de 1941, un operador alemán encargado de realizar comunicaciones a través de las Lorenz envió un mensaje cifrado de un tamaño bastante considerable, unos 4.000 caracteres tecleados directamente sin utilizar las tiras de papel, desde la ciudad de Atenas con destino Viena. El caso es que una vez enviado pacientemente el mensaje carácter a carácter, parece ser que el operador recibió otro de respuesta en alemán, solicitándole que por favor volviera a enviarlo de nuevo ya que no había sido recibido correctamente. Fue entonces cuando el operador cometió el error táctico de enviar nuevamente el mensaje con un idéntico indicador (3) (HQIBPEXEZMUG) de la máquina Lorenz a como lo había hecho la vez anterior, excepto que esta vez abrevió algunas de las palabras eliminando algunas letras de la terminación de las mismas. Este hecho constituyó un error gravísimo, ya que no respetó una de las normas básicas de la criptología, lo que puso de manifiesto una debilidad en las Lorenz, permitiendo que el equipo de criptoanalistas de Bletchley Park liderados por John Tiltman (1894-1982) comenzaran a analizar el código Tunny.

John Hessel Tiltman

Tiltman, que gozaba de una reputada posición debido a sus trabajos contra las cifras militares japonesas, y algunas cifras alemanas entre otras, comenzó su análisis mediante una ingeniosa técnica. Si por ejemplo sumamos los caracteres J y P, obtenemos L; si a L le sumamos nuevamente P, obtenemos J, que era el carácter de partida.

×× · × · + · ×× · × = × · ××× ⇒ × · ××× + · ×× · × = ×× · × ·

Una vez sumados los dos textos cifrados, obtuvo una cadena de caracteres que resultaba ser la suma de dos textos planos, esto es si tenemos P1 y P2, textos planos, y les sumamos la secuencia K para obtener los textos cifrados C₁ y C₂ (P_i + K = C_i, i = 1, 2), entonces al sumar los dos textos cifrados, obtendremos la suma de los dos textos planos, ya que en virtud de la propiedad anterior C₁ + C₂ = (P₁ + K) + (P₂ + K), pero. John Hessel Tiltman. como hemos visto antes K + K = 0 (considerando por 0 el elemento neutro de esta aritmética). En este punto es necesario observar que si realizamos la suma de dos textos cifrados idénticamente iguales con la misma clave, el resultado es una secuencia de elementos neutros, por lo que los cambios pequeños introducidos por el operador del mensaje fueron lo suficientemente significativos para poder realizar el ataque criptológico.

Una vez realizó la eliminación de la secuencia de cifrado, Tiltman sabía que cada carácter del texto resultante era la suma de otros dos que en el mensaje original distaban unas pocas posiciones. Comenzó entonces la tarea que requería una mayor inspiración, que consistía en adivinar qué palabras combinadas (o sumadas) con el texto obtenido, podían revelar el mensaje original. Tiltman ya había demostrado sus cualidades “adivinatorias” en anteriores ocasiones, una habilidad adquirida y entrenada a lo largo de sus años de servicio. Uno de sus muchos logros, había consistido en la desencriptación de un mensaje cifrado mediante el código de Vernam en el verano de 1941. Un resultado directo de la estrategia seguida por Tiltman, tarea ésta que le había llevado 10 días, significaba que sumando el texto plano a cualquiera de los dos mensajes cifrados interceptados, se obtenía la secuencia de caracteres de la clave utilizada para cifrar los mensajes. Fue en ese instante cuando todo el equipo de Tiltman aunó esfuerzos con la esperanza de intentar hallar alguna lógica que explicara la aparente aleatoriedad de los caracteres obtenidos con las Lorenz.

¿Era posible que los alemanes hubieran inventado un sistema que generara secuencias aleatorias de manera sincronizada? Si fuera así, no cabría menor esperanza de éxito en la empresa en la que los británicos se acababan de enrolar. Por el contrario, mantenían el deseo de encontrar algún tipo de sistematización similar al que habían sido capaces de obtener con la Enigma. Sin embargo, el gran inconveniente con el que contaban era que nadie había llegado a ver nunca ninguna máquina similar, y la poca información que tenían sobre ella era muy pobre. Con este desamparado panorama, y tras muchos intentos infructuosos de descubrir algún tipo de sistematización que explicara aquella aparente aleatoriedad, en las navidades de 1941, Gerry Morgan, director de investigación del departamento de Tiltman, se acercó a la mesa de William Thomas Tutte (1917-2002), un estudiante de química de la Unversidad de Cambridge, y le dijo “Mira a ver que puedes hacer con esto . . . ”. Tutte, que había sido rechazado en Bletchley Park para la desencriptación de Enigma, fue reclutado por el propio Tiltman para su equipo de criptoanalistas. Tutte ya tenía experiencia en tareas criptoanalíticas con el código Hagelin y la máquina sueca C-36. De inmediato se puso a trabajar para averiguar el funcionamiento de las Lorenz. Paradójicamente, a diferencia de las Enigma, la ruptura del código de las Lorenz fue relativamente más sencilla.

William Thomas Tutte

Tutte, que estaba muy familiarizado con el método de Kasiski ya que había sido instruido en él durante su fase de reclutamiento, comenzó estudiando patrones de repetición de dicho mensaje. Recordemos que aunque el método de Kasiski estuviera diseñado para romper la cifra Vigènere, podía resultar muy útil en general a la hora de encontrar comportamientos periódicos sistemáticos de la clave en multitud de cifrados. Tutte colocó al principio los caracteres cifrados en código Baudot en vertical en siete filas de 575 caracteres cada una. El porqué utilizó esta cantidad es debido a que al colocar todos los caracteres del mensaje cifrado en un rectángulo, observó ciertas repeticiones primero cada 23 posiciones y después cada 25. Tras multiplicar estos números (23 × 25 = 575), consideró oportuno realizar esta suposición. Al principio no parecía haber demasiadas coincidencias, pero para su sorpresa observó que existían algunas repeticiones en una diagonal, y que parecía que obtendría mejores resultados si configuraba el mensaje con un periodo de 574 caracteres. Así lo hizo y observó con gran satisfacción que se producían un gran número de repeticiones de patrones de longitud 5 o 6. Entonces realizó un nuevo intento con un periodo de 41, ya que éste es un factor primo de 574, y los resultados fueron asombrosamente aún mejores. Poco a poco fue descubriendo la configuración de funcionamiento de las Lorenz, lo cual era sorprendente ya que nunca tuvo delante ninguna de estas máquinas.

La máquina Lorenz contaba con lo que hoy día conocemos como generador de números aleatorios, que no es otra cosa que una clase de algoritmo que se utiliza en la programación de los modernos ordenadores para la obtención de números pseudoaleatorios. Desde un punto de vista mecánico cada una de estas ruedas o pinwheels poseía un cierto número de posiciones sobre su periferia con un perno o pin que admitía dos posiciones, on u off (encendido o apagado), que durante el giro de la rueda afectaban o no a otras partes de la máquina generándose secuencias de pulsos on/off o si se prefiere secuencias de bits 1/0. El número de pernos o pins era variable en cada rueda, de modo que χ1, χ2, χ3, χ4 y χ5 tenían 41, 31, 29, 26 y 23 respectivamente, mientras que ψ1, ψ2, ψ3, ψ4 y ψ5 presentaban 43, 47, 51, 53 y 59 cada una de ellas, y finalmente las dos ruedas motoras µ₁ y µ₂ contaban con 37 y 61 respectivamente. Las ruedas χ giraban todas una posición para cada carácter. Las ruedas ψ también giraban todas a la vez, pero no con cada carácter. Su movimiento estaba controlado por las dos ruedas motoras µ. En las SZ40 la rueda µ₁ giraba una posición con cada carácter, pero la rueda µ₂ únicamente giraba cuando el pin de la periferia estaba en la posición de encendido on. Si el pin de la rueda µ₂ estaba encendido, entonces todas las ruedas ψ giraban. El orden de las ruedas era (de izquierda a derecha): χ1, χ2, χ3, χ4, χ5, µ2, µ1, ψ1, ψ2, ψ3, ψ4, ψ5. Los modelos SZ42A y SZ42B estaban dotados de un mecanismo aún más complejo. Como puede observarse el número de pins de una rueda era un número primo relativo al de otras ruedas, ya que de esta forma se hacía máximo el periodo combinado de todas las ruedas, y de este modo el patrón de repetición. Con un total de 501 pines, esto suponía 2501 que es aproximadamente 10151 posibilidades de cifrado con 1, 6 × 1015 posiciones iniciales de las ruedas posibles. Sin embargo, si los cinco impulsos se consideraban de manera independiente, los números resultantes eran más manejables. El producto del periodo de rotación de cualquier par de ruedas χ supone entre 41 × 31 = 1271 y 26 × 23 = 598. Esta clase de ingenio mecánico se considera hoy en día como uno los predecesores de lo que en electrónica y en criptografía se conoce con el nombre de registros de desplazamiento alimentados linealmente (en inglés Linear Feedback Shift Registers, abreviadamente LFSK). Cuatro meses después de haberle sido encomendada la tarea a Tutte, y una vez el código Lorenz había sido descifrado, en Bletchley Park se mandó construir una máquina electro-mecánica, a la que se le bautizó con el nombre de máquina Tunny, cuya finalidad era precisamente sistematizar las tareas de descodificación de las Lorenz.

Exámen de periocidad de la rueda χ1, repeticiones de Kasiski: A, B, C. Secuencias escritas en filas de 41 caracteres de longitud. Manuscrito de Tutte.

En una primera instancia, Tutte había desarrollado un método para establecer la configuración inicial de las Lorenz “a mano”. Sin embargo este método no resultaba operativo, ya que el descifrado de un simple mensaje podía llegar a alargarse varias semanas en el tiempo, por lo que en la mayoría de las ocasiones el mensaje había perdido ya todo el interés, pues hacía referencia a órdenes ya obsoletas, de las cuales era imposible sacar ninguna ventaja desde el punto de vista estratégico. Por ello, era necesario desarrollar un nuevo método capaz de obtener rápidamente si no el mensaje plano íntegro, sí una gran mayoría de caracteres que ayudaran a la inteligencia británica a adelantarse a los acontecimientos.

En noviembre de 1942, Tutte desarrolló un ingenioso método con el que si bien no se obtenía la traducción exacta de los mensajes, sí que lo hacía en una gran proporción. Este método fue bautizado con el nombre de Método Estadístico. Los cálculos necesarios se llevaban a cabo mediante la comparativa de dos secuencias de caracteres en código Baudot, puntos y cruces (similar a 1 y 0 como anteriormente se hizo referencia), y llevando a cabo un recuento del número de veces que cada uno de ellos tenía un punto o una cruz en la misma posición. Tutte puso en conocimiento de Max Newman, jefe de la sección de desarrollo mecánico en Bletchley Park, y éste le sugirió utilizar contadores electrónicos de alta velocidad con el fin de automatizar el proceso.

3. Con anterioridad a octubre de 1942, los operadores alemanes, conforme al libro de códigos que les era entregado mensualmente, establecían en el preámbulo del mensaje cifrado con un código Tunny una secuencia de 12 caracteres que se denominaba indicador, relacionado directamente con la configuración inicial de cada una de las 12 ruedas de las Lorenz. En ocasiones escribían 12 nombres, por ejemplo Martha, Gustav, Otto, Ludwig, . . . , que se correspondía con el indicador “MGOL . . . ”. Si el emisor escribía el anterior indicador, el receptor sabía que la primera rueda ψ debía configurarse en la posición X de acuerdo al libro de códigos, siendo X la configuración de la letra M en el libro de códigos para el día de emisión del mensaje.

Véase también

5. Final de los protagonistas de Enigma

Principal

Evolución de la criptografía