El cifrado mediante rotores Como cualquier otra máquina criptográfica, las denominadas "máquinas de rotores" tenían la misión de tomar un mensaje original escrito en texto llano y utilizando una clave convertirlo en un mensaje cifrado que podía enviarse a través de medios abiertos o fácilmente interceptables, como eran las ondas de radio o las lineas telegráficas. Una vez en poder del destinatario, la misma clave servía para entrar el mensaje cifrado en otra máquina semejante y que de ella saliera el mensaje original. Hablando en términos criptográficos, las cifradoras de rotores funcionaban por el "método de sustitución de caracteres", que de forma sencilla podemos explicar con el símil de escribir dos alfabetos en sendas líneas con los caracteres alineados en vertical, pero mientras el primero está ordenado de la A la Z, el segundo está desordenado de forma aleatoria, de manera que por ejemplo a la A del primero le corresponda una M del segundo, a la B del primero una O del segundo, y así sucesivamente. De esta forma, para cifrar nuestro mensaje bastará con recorrer sus letras, localizarlas en la primera línea y sustituirlas por las equivalentes de la segunda.   Sustituciones monoalfabéticas ALFABETO ORIGINAL    A B C D E F G H I J K L M N O P Q R S T U V W X Y Z ALFABETO SUSTITUTO M O N P A T Z C R D Y U H W G I B V S Q E K X L F J   Aquí la palabra GENERAL quedaría cifrada como ZAWAVMV Sin embargo, de este proceso resultaría una "sustitución monoalfabética" muy simple y fácil de criptoanalizar, porque el segundo alfabeto es siempre el mismo y bastaría con tomar un mensaje cifrado de cierta longitud y efectuar un análisis de la frecuencia con que aparecen los caracteres en el idioma de escritura para encontrar las equivalencias entre caracteres. La máquinas de rotores, en cambio, utilizaban una sustitución denominada "polialfabética", mucho más segura que la anterior, en que el segundo alfabeto cambia cada vez que introducimos un nuevo carácter siguiendo una secuencia muy larga y difícil de prever. Por ejemplo, a continuación se muestra un ejemplo de sustitución polialfabética, en este caso de 5 alfabetos   Sustituciones polialfabéticas ALFABETO ORIGINAL A B C D E F G H I J K L M N O P Q R S T U V W X Y Z ALFABETO SUSTITUTO-1 M O N P A T Z C R D Y U H W G I B V S Q E K X L F J ALFABETO SUSTITUTO-2 T U S M D Q A B P V Z X H N E W F C G K O R I L J Y ALFABETO SUSTITUTO-3 E M G A K V L T H W R B S C O I Z N Q X F Y J P D U ALFABETO SUSTITUTO-4 O U F H V R A J B G S Z Y T E P W Q D I L M C K X N ALFABETO SUSTITUTO-5 F G X H C P D K I Q R U V J L Y Z M A B E N O W S T   Aquí la palabra GENERAL quedaría cifrada como ZDCVMMX, siguiendo el proceso: - La sustitución de G se busca en el alfabeto sustituto-1, resultando la Z - La sustitución de E se busca en el alfabeto sustituto-2, resultando la D - La sustitución de N se busca en el alfabeto sustituto-3, resultando la C - La sustitución de E se busca en el alfabeto sustituto-4, resultando la V - La sustitución de R se busca en el alfabeto sustituto-5, resultando la M - La sustitución de A se busca en el alfabeto sustituto-1, resultando la M - La sustitución de L se busca en el alfabeto sustituto-2, resultando la X De esta forma el análisis de frecuencias queda notablemente dificultado. Sin embargo, las sustituciones polialfabéticas tampoco son nuevas en criptografía y desde mediados del siglo XIX existen métodos para analizarlas, especialmente si el número de alfabetos es más pequeño que la longitud del mensaje, como en este caso. Por este motivo la seguridad del sistema polialfabético estriba en que el número de alfabetos sea muy grande, incluso de billones, que es precisamente lo que consiguieron e incluso superaron algunas máquinas de rotores. ¿Pero cómo operaban realmente dichas máquinas? ...Pues mediante una serie de cilindros con contactos eléctricos en cada lado denominados "rotores", que al girar de cierta manera iban cambiando las "sustituciones" entre la letra de entrada y la de salida. Un rotor es básicamente un cilindro que en sus dos caras planas dispone de sendos círculos de contactos metálicos, normalmente 26, que corresponden al número de caracteres del alfabeto internacional. Sin embargo, los contactos enfrentados de ambas caras no están conectados entre sí de forma paralela, sino que por ejemplo, si tomamos las sustituciones en número de orden que se dan entre nuestro "ALFABETO ORIGINAL" y el "ALFABETO SUSTITUTO-1", el contacto 1 de la cara de entrada estaría conectado al 13 de la de salida (salto +12), el contacto 2 de la entrada estaría conectado al 15 de salida (salto +13) y así, como muestra el siguiente gráfico, podríamos encontrar las equivalencias o saltos sucesivos hasta llegar al 26.   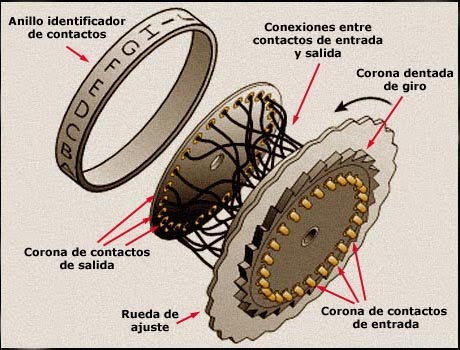Nº de orden y saltos entrada/salida de nuestro Rotor 1 Nº ORDEN ALFABETO    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 ALFABETO ORIGINAL   A B C D E F G H I J K L M N O P Q R S T U V W X Y Z ALFABETO SUSTITU-1     M O N P A T Z C R D Y U H W G I B V S Q E K X L F J SALTO ENT/SALIDA   12 13 11 12 12 14 19 -5 9 -6 14 9 -5 9 -8 -7 -15 4 0 -3 -16 -11 1 -12 -19 -16   En los rotores de Enigma y máquinas similares los contactos se identificaban mediante un anillo externo troquelado con letras de la A a la Z o números del 1 al 26.

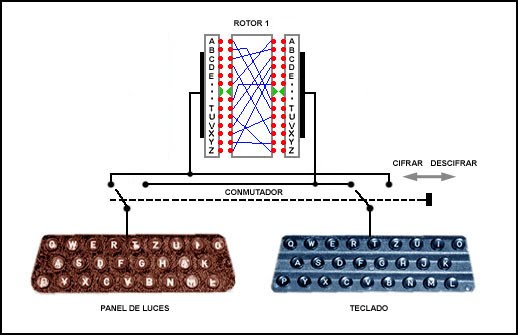
Imaginémonos ahora que este rotor, que llamaremos R1, está insertado entre un teclado de contactos eléctricos y un panel de bombillas que iluminan sus respectivas letras. Si el rotor tuviera las conexiones paralelas entre los contactos de entrada y de salida (todos sus saltos fueran 0), al pulsar nosotros la tecla A (que en este momento va al contacto 1 de entrada de R1) se iluminaría la bombilla A correspondiente en la salida, e igual ocurría con la tecla B (que va al contacto 2 de entrada de R1) y a la bombilla B, pero como ya hemos dicho que los contactos de entrada y salida están interconectados de distinta forma, en el momento que apretemos la tecla A, la corriente irá hacia el contacto 1 rotor R1, pero con la "sustitución" que le hemos asignado a este contacto es "salto+12" y por tanto saldrá por el contacto 13 del otro lado, con lo cual iluminará la letra M. Si ahora volvemos a pulsar la letra A podríamos pensar que la sustitución será la misma, pero resulta que el rotor dispone en su cara de entrada de una corona dentada tipo trinquete y la base de la máquina tiene un mecanismo que a cada pulsación del teclado actúa sobre dicha corona, provocando que el rotor avance un paso. De esta manera, en la siguiente pulsación ya no tendremos el contacto 1 enfrentado a la posición A, sino el 2 (con un salto +13), y por tanto, en este caso la A va a transformarse en una N.   <- Diagrama interno de un rotor mostrando las distintas partes

En una máquina de estas características (recordemos que no estamos hablamos de ninguna marca ni modelo concreto), el descifrado del mensaje deberá hacerse invirtiendo el sentido de la corriente, con el teclado conectado a la cara de "salida" del rotor, y el panel de luces a su cara de "entrada". Para conseguir esta modificación, y tal como muestra el diagrama izquierdo, se disponía de un conmutador que mediante una simple palanca efectuaba el cambio de conexiones. Las salidas del conmutador van a sendos colectores fijos cuya misión en conectar con su rotor inmediato. Vemos también el rotor con sus respectivos contactos en cada cara y las interconexiones que crean el cifrado por sustitución, aunque por problemas de espacio en el dibujo sólo he incluido 13 de los 26 contactos que corresponden a los 26 caracteres del alfabeto completo. El eje de giro del rotor está representado en verde, y podemos darnos cuenta como al girar este elemento, el "camino eléctrico" entre el alfabeto de entrada y el de salida cambia por completo, lo cual constituye la esencia de este cifrado.   <- Diagrama esquemático de una máquina cifradora de un solo rotor, insertado entre un teclado y un panel indicador de bombillas

Rotores típicos de Enigma, mostrado los contactos de entrada provistos de muelles, la corona dentada de trinquete, la rueda ondulada de ajuste y el anillo identificador de contactos, es este caso troquelado con números

El mismo rotor, mostrando los contactos de salida y la muesca que provoca el arrastre del siguiente rotor

Este sistema es por tanto polialfabético porque a cada paso de giro del rotor las sustituciones A-Z de entrada y salida serán distintas... al menos hasta que el rotor haya dado una revolución completa y tras el paso 26 vuelva a repetir las sustituciones iniciales, lo cual implicaría disponer de sólo 26 alfabetos e igual número de claves que adoptarían la forma de una letra de la A la Z o de un número de 1 a 26, y que no impedirían a cualquier criptólogo aficionado decodificar el mensaje con relativa facilidad. 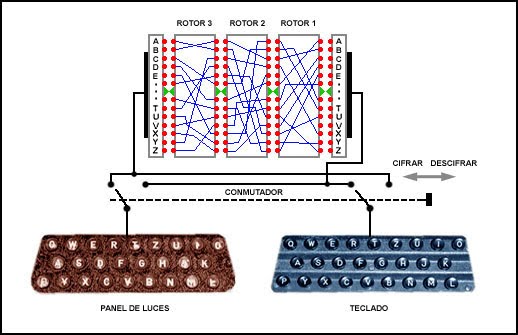...Pero por suerte podremos mejorar esta limitación insertando otro rotor con otras equivalencias entre el anterior y el panel de bombillas, de tal forma que la salida del primero vaya a la entrada del segundo, resultando una sustitución total que será suma de la individual de cada rotor. El sistema de giro de rotores será tipo serie, es decir, mientras el rotor R1 se mueve un paso a cada pulsación de una tecla, el rotor R2 sólo se moverá un paso a cada revolución completa de R1. Para conseguir esto, los rotores disponen de una muesca llamada "notch", situada en cierta posición, y cuando a causa del giro dicha muesca encaja en un diente o palanca del mecanismo base de la máquina, éste hará avanzar un paso el siguiente rotor, actuado sobre su corona dentada de trinquete de la cara de entrada.

Con la disposición de dos rotores el ciclo de posibilidades pasa de sólo 26 a 676 (26x26) alfabetos, siendo la clave del mensaje la posición inicial de los dos rotores en forma de dos letras (ejemplo Q-L), p dos cifras de 1 a 26 (ejemplo 17-12). Naturalmente, si añadimos un tercer rotor el número de alfabetos será de 17.576 (26x26x26), con claves de tres letras de A a la Z o de tres números del 1 a 26. Obviamente, para decodificar un mensaje salido de una máquina de este tipo, no sólo deberemos cambiar el conmutador a la posición "descifrado" para invertir el sentido de la corriente, sino que también deberemos colocar los rotores en posiciones iniciales correspondientes a la clave (ejemplo B-X-N o 3-16-21, antes de introducirle el primer carácter cifrado.

Éste sería el funcionamiento básico de una máquina de rotores, aunque como iremos viendo los modelos reales casi nunca fueron tan sencillos e incorporaban otras posibilidades y elementos adicionales para conseguir mayor fortaleza del cifrado, principalmente aumentando la cantidad de claves disponibles.             <- Diagrama esquemático de una máquina de tres rotores, insertados en serie entre un teclado y un panel indicador de bombillas

? Referencia: La Web de Anilandro

 

Más información

• Los rotores
• Rotores: identificación de clase y cableado
• Página principal de Enigma